【题目】已知:如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象交于点
)的图象交于点![]() .
.![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() . 一次函数的图象分别交
. 一次函数的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、点
、点![]() ,且
,且![]() ,
,![]() .
.
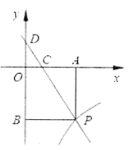
(1)求点![]() 的坐标;
的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当![]() 取何值时,一次函数的值小于反比例函数的值?
取何值时,一次函数的值小于反比例函数的值?
参考答案:
【答案】(1)![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() ,
, ![]() ; (3)当
; (3)当![]() 时,一次函数的值小于反比例函数的值.
时,一次函数的值小于反比例函数的值.
【解析】
(1)本题需先根据题意一次函数与y轴的交点,从而得出D点的坐标.
(2)本题需先根据在Rt△COD和Rt△CAP中,![]() ,OD=3,再根据S△DBP=27,从而得出BP得长和P点的坐标,即可求出结果.
,OD=3,再根据S△DBP=27,从而得出BP得长和P点的坐标,即可求出结果.
(3)根据图形从而得出x的取值范围即可.
解:(1)∵一次函数![]() 与
与![]() 轴相交,
轴相交,
∴令![]() ,解得
,解得![]() ,
,
∴![]() 的坐标为
的坐标为![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
∴![]() ,
,
故![]() ,
,
把![]() 坐标代入
坐标代入![]() ,得到
,得到![]() ,
,
则一次函数的解析式为:![]() ;
;
把![]() 坐标代入反比例函数解析式得
坐标代入反比例函数解析式得![]() ,
,
则反比例解析式为:![]() ;
;
(3)如图:

根据图象可得: ,
,
解得:![]() 或
或 ![]()
故直线与双曲线的两个交点为![]() ,
,![]() ,
,
∵![]() ,
,
∴当![]() 时,一次函数的值小于反比例函数的值.
时,一次函数的值小于反比例函数的值.
-
科目: 来源: 题型:
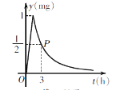
查看答案和解析>>【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=
 (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于
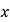 的方程
的方程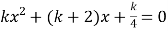 有两个不相等的实数根.
有两个不相等的实数根.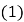 求实数
求实数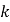 的取值范围;
的取值范围; 是否存在实数
是否存在实数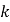 ,使方程的两个实数根之和等于两实数根之积的算术平方根?若存在,求出
,使方程的两个实数根之和等于两实数根之积的算术平方根?若存在,求出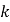 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
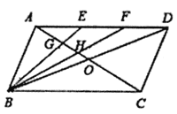
查看答案和解析>>【题目】如图,在
 中,对角线
中,对角线 、
、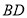 相交于点
相交于点 ,点
,点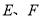 是
是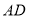 上的点,且
上的点,且 . 连接
. 连接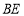 、
、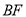 ,使它们分别与
,使它们分别与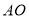 相交于点
相交于点 .
. 
(1)求
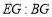 的值;
的值;(2)求证:
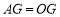 ;
;(3)设
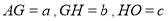 ,求
,求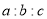 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD,∠A=60°,AB=6,点E,F分别是AB,BC边上沿某一方向运动的点,且DE=DF,当点E从A运动到B时,线段EF的中点O运动的路程为_____.
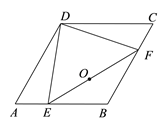
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了准备“迎新活动”,用700元购买了甲、乙两种小礼品260个,其中购买甲种礼品比乙种礼品少用了100元.
(1)购买乙种礼品花了______元;
(2)如果甲种礼品的单价比乙种礼品的单价高20%,求乙种礼品的单价.(列分式方程解应用题)
相关试题

