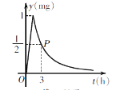
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
参考答案:
【答案】(1)y=![]() t(0≤t≤
t(0≤t≤![]() ) (2)6小时
) (2)6小时
【解析】
(1) 将点![]() 代入函数关系式
代入函数关系式![]() , 解得
, 解得![]() , 有
, 有![]()
将![]() 代入
代入![]() , 得
, 得![]() , 所以所求反比例函数关系式为
, 所以所求反比例函数关系式为![]() ;
;
再将![]() 代入
代入![]() , 得
, 得![]() ,所以所求正比例函数关系式为
,所以所求正比例函数关系式为![]() .
.
(2) 解不等式![]() , 解得
, 解得![]() ,
,
所以至少需要经过6小时后,学生才能进入教室.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(2,2)关于直线y=k
 (k>0)的对称点恰好落在x轴的正半轴上,则k的值是_____.
(k>0)的对称点恰好落在x轴的正半轴上,则k的值是_____.
-
科目: 来源: 题型:
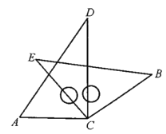
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起(其中,
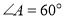 ,
,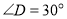 ;
;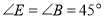 ).
).
(1)①若
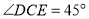 ,则
,则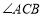 的度数为_____________;
的度数为_____________;②若
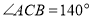 ,则
,则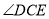 的度数为_____________.
的度数为_____________.(2)由(1)猜想
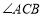 与
与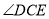 的数量关系,并说明理由.
的数量关系,并说明理由.(3)当
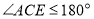 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出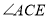 角度所有可能的值(不必说明理由);若不存在,请说明理由.
角度所有可能的值(不必说明理由);若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
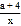 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+
的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+ =0的根的情况是________________.
=0的根的情况是________________.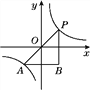
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于
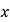 的方程
的方程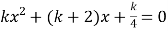 有两个不相等的实数根.
有两个不相等的实数根.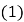 求实数
求实数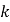 的取值范围;
的取值范围; 是否存在实数
是否存在实数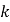 ,使方程的两个实数根之和等于两实数根之积的算术平方根?若存在,求出
,使方程的两个实数根之和等于两实数根之积的算术平方根?若存在,求出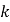 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
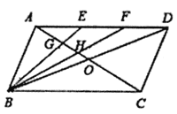
查看答案和解析>>【题目】如图,在
 中,对角线
中,对角线 、
、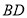 相交于点
相交于点 ,点
,点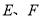 是
是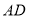 上的点,且
上的点,且 . 连接
. 连接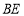 、
、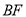 ,使它们分别与
,使它们分别与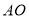 相交于点
相交于点 .
. 
(1)求
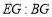 的值;
的值;(2)求证:
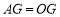 ;
;(3)设
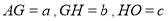 ,求
,求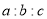 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,一次函数
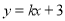 的图象与反比例函数
的图象与反比例函数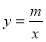 (
(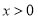 )的图象交于点
)的图象交于点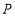 .
.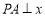 轴于点
轴于点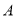 ,
,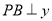 轴于点
轴于点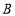 . 一次函数的图象分别交
. 一次函数的图象分别交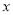 轴、
轴、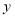 轴于点
轴于点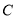 、点
、点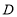 ,且
,且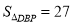 ,
,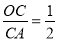 .
. 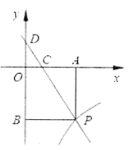
(1)求点
 的坐标;
的坐标;(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当
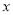 取何值时,一次函数的值小于反比例函数的值?
取何值时,一次函数的值小于反比例函数的值?
相关试题

