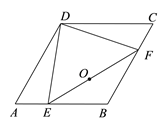
【题目】如图,菱形ABCD,∠A=60°,AB=6,点E,F分别是AB,BC边上沿某一方向运动的点,且DE=DF,当点E从A运动到B时,线段EF的中点O运动的路程为_____.
参考答案:
【答案】3或3![]()
【解析】分析:
连接AC、BD相交于点P,由已知条件易得AC=![]() ,BD=6,再根据题意,分①点F由点B向点C运动;②点F由点C向点B运动两种情况,结合已知条件进行分析解答即可.
,BD=6,再根据题意,分①点F由点B向点C运动;②点F由点C向点B运动两种情况,结合已知条件进行分析解答即可.
详解:
如图,连接AC、BD相交于点P,
∵四边形ABCD是菱形,AB=6,∠DAB=60°,
∴∠BAC=30°,AC=2AP,BD=2PB,△ABD和△CBD都是等边三角形,
∴AP=AB·cos30°=![]() ,BP=AB·sin30°=3,AD=BD=CD,
,BP=AB·sin30°=3,AD=BD=CD,
∴AC=![]() .
.

(1)若点F是由点B向点C运动的,则由图1和题意可知,当点E与点A重合时,点F与点B重合,此时点O与线段AB的中点M重合;而当点E移动到与点B重合时,点F移动到与点C重合,此时点O与线段BC的中点N重合,
∴在点E由点A向点B移动,且点F由点B向点C移动的过程后,线段EF的中点O移动所经过的路线是△ABC的中位线MN,
∴在这种情况下,点O移动的路程=MN=![]() AC=
AC=![]() ;
;
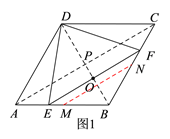
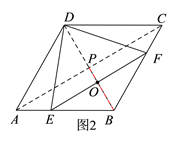
(2)若点F是由点C向点B运动的,则由图2和题意可知,当点E与点A重合时,点F与点C重合,此时点O与点P重合;而当点E移动到与点B重合时,点F也移动到与点B重合,此时点O与点B重合,
∴在点E由点A向点B移动,且点F由点C向点B移动的过程中,线段EF的中点O移动所经过的路线是线段PB,
∴在这种情况下,点O移动的路程=PB=3.
故答案为:![]() 或3.
或3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,对角线
中,对角线 、
、 相交于点
相交于点 ,点
,点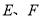 是
是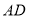 上的点,且
上的点,且 . 连接
. 连接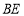 、
、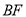 ,使它们分别与
,使它们分别与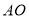 相交于点
相交于点 .
. 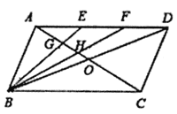
(1)求
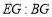 的值;
的值;(2)求证:
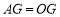 ;
;(3)设
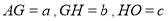 ,求
,求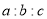 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,一次函数
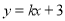 的图象与反比例函数
的图象与反比例函数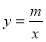 (
(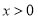 )的图象交于点
)的图象交于点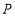 .
.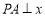 轴于点
轴于点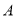 ,
,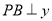 轴于点
轴于点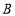 . 一次函数的图象分别交
. 一次函数的图象分别交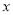 轴、
轴、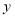 轴于点
轴于点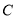 、点
、点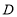 ,且
,且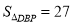 ,
,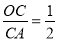 .
. 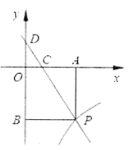
(1)求点
 的坐标;
的坐标;(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当
 取何值时,一次函数的值小于反比例函数的值?
取何值时,一次函数的值小于反比例函数的值? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了准备“迎新活动”,用700元购买了甲、乙两种小礼品260个,其中购买甲种礼品比乙种礼品少用了100元.
(1)购买乙种礼品花了______元;
(2)如果甲种礼品的单价比乙种礼品的单价高20%,求乙种礼品的单价.(列分式方程解应用题)
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年农历五月初五是我国的传统佳节“端午节”,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售量较好的栗子粽、豆沙粽、红枣粽、蛋黄粽、大肉粽(以下分别用A,B,C,D,E表示)这五种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅不完整统计图.
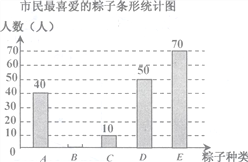
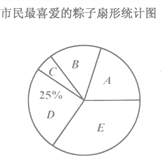
根据以上统计图解答问题:
(1)本次被调查的市民有多少人,请补全条形统计图;
(2)扇形统计图中大肉粽对应的圆心角是_____度;
(3)若该市有居民约200万人,估计其中喜爱大肉粽的有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=6
 与双曲线y=
与双曲线y= (k≠0,且
(k≠0,且 >0)交点A,点A的横坐标为2.
>0)交点A,点A的横坐标为2.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上的点,且点B的纵坐标是6,连接OB,AB.求三角形△AOB的面积.
相关试题

