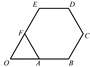
【题目】如图,正六边形ABCDEF的边长为![]() ,延长BA,EF交于点O.以O为原点,以边AB所在的直线为
,延长BA,EF交于点O.以O为原点,以边AB所在的直线为![]() 轴建立平面直角坐标系,则直线DF与直线AE的交点坐标是(_______).
轴建立平面直角坐标系,则直线DF与直线AE的交点坐标是(_______).
参考答案:
【答案】(2![]() ,4)
,4)
【解析】试题解析:如答图,连接AE,DF,
∵正六边形ABCDEF的边长为![]() ,延长BA,EF交于点O,
,延长BA,EF交于点O,
∴△AOF是等边三角形,则AO=FO=FA=![]() .
.
∵以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,∠EOA=60°,EO=FO+EF=![]() ,
,
∴∠EAO=90°,∠OEA=30°.∴AE=![]() cos30°=6.∴F(
cos30°=6.∴F(![]() ,3),D(
,3),D(![]() ,6).
,6).
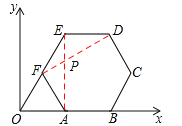
设直线DF的解析式为:y=kx+b,
则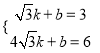 ,解得:
,解得: 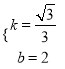 .
.
∴直线DF的解析式为: ![]() .
.
∵当x=![]() 时,
时, ![]() ,
,
∴直线DF与直线AE的交点坐标是:(![]() ,4).
,4).
故答案为:(![]() ,4).
,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备建一条5米宽的文化长廊,并按下图方式铺设边长为1米的正方形地砖,图中阴影部分为彩色地砖,白色部分为普通地砖.

(1)如果长廊长8米,则需要彩色地砖______块,普通地砖______块;
如果长廊长9米,则需要彩色地砖______块,普通地砖______块;
(2)如果长廊长2a米(a为正整数),则需要彩色地砖______块;
如果长廊长(2a+1)米(a为正整数),则需要彩色地砖______块;
(3)购买时,恰逢地砖市场地砖促销,彩色地砖原价为100元/块,普通地砖原价为40元/块,优惠方案为:买一块彩色地砖赠送一块普通地砖.
①如果长廊长x米(x为整数),用含x代数式表示购买地砖所需的钱数;
②当x=51米时,求购买地砖所需钱数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑摩托车从邮局出发,先向西骑行2km到达A村,继续向西骑行3km到达B村,然后向东骑行9km到达C村,最后回到邮局.
(1)以邮局为原点,向东方向为正方向,用1cm表示1km,画出数轴,并在该数轴上表示A、B、C三个村庄的位置;
(2)C村离A村有多远?
(3)若摩托车的油耗为每千米0.03L,求邮递员这次出行的耗油量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线a 、b被直线c所截,现给出下列四种条件:
①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a∥b的条件的序号是( )

A. ①② B. ①③ C. ①④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为4的正方形ABCD外切于⊙O,切点分别为E、F、G、H.则图中阴影部分的面积为______.

-
科目: 来源: 题型:
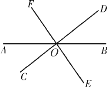
查看答案和解析>>【题目】如图,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_________,∠AOC的邻补角是_______.若∠AOC=50°,则∠BOD=__________,∠COB=______________.
-
科目: 来源: 题型:
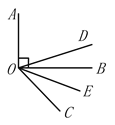
查看答案和解析>>【题目】如图,DO平分∠AOC,OE平分∠BOC,若OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________; 当∠BOC=60°,∠DOE=_______________;
(2)通过上面的计算,猜想∠DOE的度数与∠AOB有什么关系,并说明理由.
相关试题

