【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,请你根据以上信息及(2)问中条件,设计出使这100台家电销售总利润最大的进货方案.
参考答案:
【答案】(1)每台空调的进价为1600元,则每台电冰箱的进价为2000元;
(2)合理的方案共有7种;当购进电冰箱34台,空调66台获利最大,最大利润为13300元;
(3)当50<k<100时,购进电冰箱40台,空调60台销售总利润最大;当0<k<50时,购进电冰箱34台,空调66台销售总利润最大;当k=50时,每种进货方案的总利润都一样.
【解析】
试题分析:(1)由题意设每台空调的进价为x元,则每台电冰箱的进价为(x+400)元,,根据商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等列方程,解方程.
(2)题目有三个要求,总利润不低于13000元,购进空调数量不超过电冰箱数量的2倍,和现实意义冰箱空调的数量必须取整数,根据这三个要求,逐一考虑,利润=单件的利润(售价-进价)×数量,总利润=电冰箱的利润+空调的利润,得到y关于x的一次函数,根据第二个要求列出不等式,在一二两个要求的范围内找到整数解.
(3)电冰箱出产价下调的k元,就是每台电冰箱利润增加k元,依据题意求出总利润y关于x的一元一次函数,由函数解析式及一次函数的性质可知,总利润的最大值由k-50的正负性决定,在此分三种情况讨论.
试题解析:(1)设每台空调的进价为x元,则每台电冰箱的进价为(x+400)元,根据题意得:![]() ,解得:x=1600,经检验,x=1600是原方程的解,x+400=1600+400=2000,
,解得:x=1600,经检验,x=1600是原方程的解,x+400=1600+400=2000,
答:每台空调的进价为1600元,则每台电冰箱的进价为2000元.
(2)设购进电冰箱x台,这100台家电的销售总利润为y元,则y=(2100﹣2000)x+(1750﹣1600)(100﹣x)=﹣50x+15000,根据题意得:![]() ,解得:
,解得:![]() ,∵x为正整数,∴x=34,35,36,37,38,39,40,∴合理的方案共有7种,即①电冰箱34台,空调66台;②电冰箱35台,空调65台;③电冰箱36台,空调64台;④电冰箱37台,空调63台;⑤电冰箱38台,空调62台;⑥电冰箱39台,空调61台;⑦电冰箱40台,空调60台;
,∵x为正整数,∴x=34,35,36,37,38,39,40,∴合理的方案共有7种,即①电冰箱34台,空调66台;②电冰箱35台,空调65台;③电冰箱36台,空调64台;④电冰箱37台,空调63台;⑤电冰箱38台,空调62台;⑥电冰箱39台,空调61台;⑦电冰箱40台,空调60台;
∵y=﹣50x+15000,k=﹣50<0,∴y随x的增大而减小,
∴当x=34时,y有最大值,最大值为:﹣50×34+15000=13300(元),
答:当购进电冰箱34台,空调66台获利最大,最大利润为13300元.
(3)当厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,
则利润y=(2100﹣2000+k)x+(1750﹣1600)(100﹣x)=(k﹣50)x+15000,
当k﹣50>0,即50<k<100时,y随x的增大而增大,∵![]() ,∴当x=40时,这100台家电销售总利润最大,即购进电冰箱40台,空调60台;
,∴当x=40时,这100台家电销售总利润最大,即购进电冰箱40台,空调60台;
当k﹣50<0,即0<k<50时,y随x的增大而减小,∵![]() ,∴当x=34时,这100台家电销售总利润最大,即购进电冰箱34台,空调66台;
,∴当x=34时,这100台家电销售总利润最大,即购进电冰箱34台,空调66台;
当k=50时,每种进货方案的总利润都一样;
答:当50<k<100时,购进电冰箱40台,空调60台销售总利润最大;当0<k<50时,购进电冰箱34台,空调66台销售总利润最大;当k=50时,每种进货方案的总利润都一样.
-
科目: 来源: 题型:
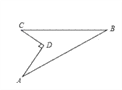
查看答案和解析>>【题目】如图所示的一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△OAB放置于平面直角坐标系xOy中,∠OAB=90°,OA=2,AB=
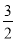 ,把△OAB沿x轴的负方向平移2OA的长度后得到△DCE.
,把△OAB沿x轴的负方向平移2OA的长度后得到△DCE.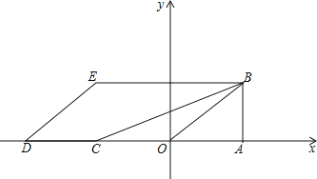
(1)若过原点的抛物线y=ax2+bx+c经过点B、E,求此抛物线的解析式;
(2)若点P在该抛物线上移动,当点p在第一象限内时,过点p作PQ⊥x轴于点Q,连接OP.若以O、P、Q为定点的三角形与以B、C、E为定点的三角形相似,直接写出点P的坐标;
(3)若点M(﹣4,n)在该抛物线上,平移抛物线,记平移后点M的对应点为M′,点B的对应点为B′.当抛物线向左或向右平移时,是否存在某个位置,使四边形M′B′CD的周长最短?若存在,求出此时抛物线的解析式;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
 是半圆
是半圆 的直径,弦
的直径,弦 ,动点
,动点 、
、 分别在线段
分别在线段 、
、 上,且
上,且 ,
, 的延长线与射线
的延长线与射线 相交于点
相交于点 、与弦
、与弦 相交于点
相交于点 (点
(点 与点
与点 、
、 不重合),
不重合), ,
, .设
.设 ,
, 的面积为
的面积为 .
.
(1)求证:
 ;
; (2)求
 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围
的取值范围(3)当
 是直角三角形时,求线段
是直角三角形时,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=6,求AE的长。

-
科目: 来源: 题型:
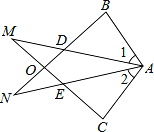
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.
-
科目: 来源: 题型:
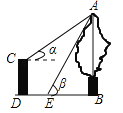
查看答案和解析>>【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)
相关试题

