【题目】如图,把△OAB放置于平面直角坐标系xOy中,∠OAB=90°,OA=2,AB=![]() ,把△OAB沿x轴的负方向平移2OA的长度后得到△DCE.
,把△OAB沿x轴的负方向平移2OA的长度后得到△DCE.
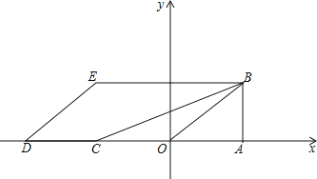
(1)若过原点的抛物线y=ax2+bx+c经过点B、E,求此抛物线的解析式;
(2)若点P在该抛物线上移动,当点p在第一象限内时,过点p作PQ⊥x轴于点Q,连接OP.若以O、P、Q为定点的三角形与以B、C、E为定点的三角形相似,直接写出点P的坐标;
(3)若点M(﹣4,n)在该抛物线上,平移抛物线,记平移后点M的对应点为M′,点B的对应点为B′.当抛物线向左或向右平移时,是否存在某个位置,使四边形M′B′CD的周长最短?若存在,求出此时抛物线的解析式;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() x2;(2)P(1,
x2;(2)P(1,![]() )或P (
)或P (![]() ,
,![]() );(3)存在,将抛物线向左平移
);(3)存在,将抛物线向左平移![]() 个单位时,四边形M′B′CD的周长最短,此时抛物线的解析式为y=
个单位时,四边形M′B′CD的周长最短,此时抛物线的解析式为y=![]() (x+
(x+![]() )2.
)2.
【解析】
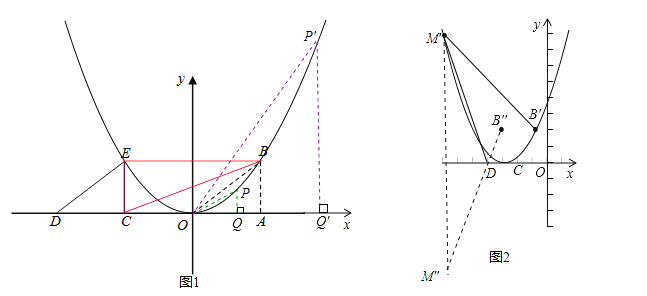
试题分析:(1)根据平移的性质求得B,E的坐标,然后利用待定系数法即可求得函数的解析式;(2)点P的坐标可设为(x,![]() ),因为∠BEC=∠OQP=90°,所以以O、P、Q为顶点的三角形与以B、C、E为顶点的三角形相似时,Q与E一定对应,然后分两种情况进行讨论:(i)△OQP∽△BEC;(ii)△PQO∽△BEC;根据相似三角形对应边成比例列出比例式,求解即可;(3)左右平移时,使M'D+CB'最短即可,那么作出点M′关于x轴对称点的坐标为M″,得到直线B″M″的解析式,令y=0,求得相应的点的坐标;进而得到抛物线顶点平移的规律,用顶点式设出相应的函数解析式,把新顶点坐标代入即可.
),因为∠BEC=∠OQP=90°,所以以O、P、Q为顶点的三角形与以B、C、E为顶点的三角形相似时,Q与E一定对应,然后分两种情况进行讨论:(i)△OQP∽△BEC;(ii)△PQO∽△BEC;根据相似三角形对应边成比例列出比例式,求解即可;(3)左右平移时,使M'D+CB'最短即可,那么作出点M′关于x轴对称点的坐标为M″,得到直线B″M″的解析式,令y=0,求得相应的点的坐标;进而得到抛物线顶点平移的规律,用顶点式设出相应的函数解析式,把新顶点坐标代入即可.
试题解析:(1)依题意得:B(2,![]() ),∵OC=2,CE=
),∵OC=2,CE=![]() ,∴E(﹣2,
,∴E(﹣2,![]() ).
).
∵抛物线经过原点和点B、E,∴设抛物线的解析式为y=ax2(a≠0).
∵抛物线经过点B(2,![]() ),∴
),∴![]() =4a.解得:a=
=4a.解得:a=![]() .
.
∴抛物线的解析式为y=![]() x2;
x2;
(2)∵点P在抛物线上,∴设点P的坐标为(x,![]() x2).
x2).
分两种情况:(i)当△OQP∽△BEC时,则![]() ,即
,即 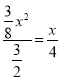 ,解得:x=1,∴点P的坐标为(1,
,解得:x=1,∴点P的坐标为(1,![]() );
);
(ii)当△PQO∽△BEC时,则![]() ,即
,即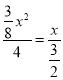 ,解得:x=
,解得:x=![]() ,∴点P的坐标为(
,∴点P的坐标为(![]() ,
,![]() ).
).
综上所述,符合条件的点P的坐标是P(1,![]() )或P (
)或P (![]() ,
,![]() );
);
(3)存在.
因为线段M′B′和CD的长是定值,所以要使四边形M′B′CD的周长最短,只要使M′D+CB′最短.
如果将抛物线向右平移,显然有M′D+CB′>MD+CB,因此不存在某个位置,使四边形M′B′CD的周长最短,显然应该将抛物线 y=![]() x2向左平移.
x2向左平移.
由题知M(﹣4,6).设抛物线向左平移了n个单位,则点M′和B′的坐标分别为
M′(﹣4﹣n,6)和B′(2﹣n,![]() ).
).
因为CD=2,因此将点B′向左平移2个单位得B″(﹣n,![]() ).
).
要使M′D+CB′最短,只要使M′D+DB″最短.点M′关于x轴对称点的坐标为M″(﹣4﹣n,﹣6).
设直线M″B″的解析式y=kx+b(k≠0),点D应在直线M″B″上,
∴直线M″B″的解析式为y=![]() ,将B″(﹣n,
,将B″(﹣n,![]() )代入,求得n=
)代入,求得n=![]() .
.
故将抛物线向左平移![]() 个单位时,四边形M′B′CD的周长最短,此时抛物线的解析式为y=
个单位时,四边形M′B′CD的周长最短,此时抛物线的解析式为y=![]() (x+
(x+![]() )2.
)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“ 六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.
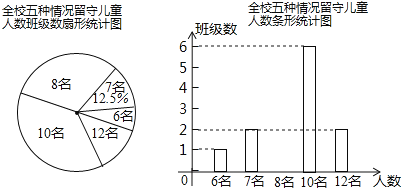
请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
-
科目: 来源: 题型:
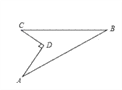
查看答案和解析>>【题目】如图所示的一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
 是半圆
是半圆 的直径,弦
的直径,弦 ,动点
,动点 、
、 分别在线段
分别在线段 、
、 上,且
上,且 ,
, 的延长线与射线
的延长线与射线 相交于点
相交于点 、与弦
、与弦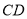 相交于点
相交于点 (点
(点 与点
与点 、
、 不重合),
不重合), ,
, .设
.设 ,
, 的面积为
的面积为 .
.
(1)求证:
 ;
; (2)求
 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围
的取值范围(3)当
 是直角三角形时,求线段
是直角三角形时,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,请你根据以上信息及(2)问中条件,设计出使这100台家电销售总利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=6,求AE的长。

相关试题

