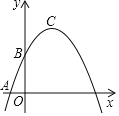
【题目】在平面直角坐标系xOy中(如图).已知抛物线y=﹣![]() x2+bx+c经过点A(﹣1,0)和点B(0,
x2+bx+c经过点A(﹣1,0)和点B(0,![]() ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)求这条抛物线的表达式;
(2)求线段CD的长;
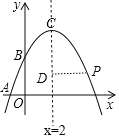
(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
参考答案:
【答案】(1)抛物线解析式为y=﹣![]() x2+2x+
x2+2x+![]() ;(2)线段CD的长为2;(3)M点的坐标为(0,
;(2)线段CD的长为2;(3)M点的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).
【解析】(1)利用待定系数法求抛物线解析式;
(2)利用配方法得到y=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ,则根据二次函数的性质得到C点坐标和抛物线的对称轴为直线x=2,如图,设CD=t,则D(2,
,则根据二次函数的性质得到C点坐标和抛物线的对称轴为直线x=2,如图,设CD=t,则D(2,![]() ﹣t),根据旋转性质得∠PDC=90°,DP=DC=t,则P(2+t,
﹣t),根据旋转性质得∠PDC=90°,DP=DC=t,则P(2+t,![]() ﹣t),然后把P(2+t,
﹣t),然后把P(2+t,![]() ﹣t)代入y=﹣
﹣t)代入y=﹣![]() x2+2x+
x2+2x+![]() 得到关于t的方程,从而解方程可得到CD的长;
得到关于t的方程,从而解方程可得到CD的长;
(3)P点坐标为(4,![]() ),D点坐标为(2,
),D点坐标为(2,![]() ),利用抛物线的平移规律确定E点坐标为(2,﹣2),设M(0,m),当m>0时,利用梯形面积公式得到
),利用抛物线的平移规律确定E点坐标为(2,﹣2),设M(0,m),当m>0时,利用梯形面积公式得到![]() (m+
(m+![]() +2)2=8当m<0时,利用梯形面积公式得到
+2)2=8当m<0时,利用梯形面积公式得到![]() (﹣m+
(﹣m+![]() +2)2=8,然后分别解方程求出m即可得到对应的M点坐标.
+2)2=8,然后分别解方程求出m即可得到对应的M点坐标.
(1)把A(﹣1,0)和点B(0,![]() )代入y=﹣
)代入y=﹣![]() x2+bx+c得
x2+bx+c得
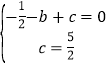 ,解得
,解得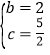 ,
,
∴抛物线解析式为y=﹣![]() x2+2x+
x2+2x+![]() ;
;
(2)∵y=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ,
,
∴C(2,![]() ),抛物线的对称轴为直线x=2,
),抛物线的对称轴为直线x=2,
如图,设CD=t,则D(2,![]() ﹣t),
﹣t),
∵线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处,
∴∠PDC=90°,DP=DC=t,
∴P(2+t,![]() ﹣t),
﹣t),
把P(2+t,![]() ﹣t)代入y=﹣
﹣t)代入y=﹣![]() x2+2x+
x2+2x+![]() 得﹣
得﹣![]() (2+t)2+2(2+t)+
(2+t)2+2(2+t)+![]() =
=![]() ﹣t,
﹣t,
整理得t2﹣2t=0,解得t1=0(舍去),t2=2,
∴线段CD的长为2;
(3)P点坐标为(4,![]() ),D点坐标为(2,
),D点坐标为(2,![]() ),
),
∵抛物线平移,使其顶点C(2,![]() )移到原点O的位置,
)移到原点O的位置,
∴抛物线向左平移2个单位,向下平移![]() 个单位,
个单位,
而P点(4,![]() )向左平移2个单位,向下平移
)向左平移2个单位,向下平移![]() 个单位得到点E,
个单位得到点E,
∴E点坐标为(2,﹣2),
设M(0,m),
当m>0时,![]() (m+
(m+![]() +2)2=8,解得m=
+2)2=8,解得m=![]() ,此时M点坐标为(0,
,此时M点坐标为(0,![]() );
);
当m<0时,![]() (﹣m+
(﹣m+![]() +2)2=8,解得m=﹣
+2)2=8,解得m=﹣![]() ,此时M点坐标为(0,﹣
,此时M点坐标为(0,﹣![]() );
);
综上所述,M点的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=10,点E、F是正方形内两点,AE=FC=6,BE=DF=8,则EF的长为( )

A.
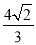 B.
B.  C.
C.  D. 3
D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】新知识一般有两类:第一类是一般不依赖于其他知识的新知识,如“数”,“字母表示数”这样的初始性知识;第二类是在某些旧知识的基础上联系,拓展等方式产生的知识,大多数知识是这一类.
(1)多项式乘多项式的法则,是第几类知识?
(2)在多项式乘多项式之前,我们学习了哪些有关的知识?(写出三条即可)
(3)请你用已有的知识,从数和形两个方面说明多项式乘多项式法则,用(a+b)(a-b)来说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是___.
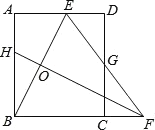
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知用2辆A型车和1辆B型车载满货物一次可运货物10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.根据以上信息,解答下列问题:
(1)用1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.

(1)如图1,如果AC=BD,求弦AC的长;
(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;
(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB∥CD,EG平分∠AEF,EH⊥EG,EH∥GF,则下列结论:①EG⊥GF;②EH平分∠BEF;③FG平分∠EFC;④∠EHF=∠FEH+∠HFD;其中正确的结论个数是( )

A.4个B.3个C.2个D.1个
相关试题

