【题目】如图,在正方形ABCD中,AB=10,点E、F是正方形内两点,AE=FC=6,BE=DF=8,则EF的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
参考答案:
【答案】B
【解析】
延长AE交DF于G,再根据全等三角形的判定得出△AGD与△ABE全等,得出AG=BE=8,由AE=6,得出EG=2,同理得出GF=2,再根据勾股定理得出EF的长.
延长AE交DF于G,如图:
∵AB=10,AE=6,BE=8,

∴△ABE是直角三角形,
∴同理可得△DFC是直角三角形,
可得△AGD是直角三角形
∴∠ABE+∠BAE=∠DAE+∠BAE,
∴∠GAD=∠EBA,
同理可得:∠ADG=∠BAE,
在△AGD和△BAE中,
 ,
,
∴△AGD≌△BAE(ASA),
∴AG=BE=8,DG=AE=6,
∴EG=2,
同理可得:GF=2,
∴EF=![]() ,
,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课
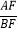 =
=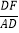 .求证:EF=EP.
.求证:EF=EP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.

(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:△MNC是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,分别过点B、C两点作过点A的直线的垂线,垂足为M、N.

(1)如图1,当M、N两点在直线BC的同侧时,求证:BM+CN=MN;
(2)如图2,当M、N两点在直线BC的两侧时,BM、CN、MN三条线段的数量关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新知识一般有两类:第一类是一般不依赖于其他知识的新知识,如“数”,“字母表示数”这样的初始性知识;第二类是在某些旧知识的基础上联系,拓展等方式产生的知识,大多数知识是这一类.
(1)多项式乘多项式的法则,是第几类知识?
(2)在多项式乘多项式之前,我们学习了哪些有关的知识?(写出三条即可)
(3)请你用已有的知识,从数和形两个方面说明多项式乘多项式法则,用(a+b)(a-b)来说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是___.
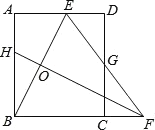
-
科目: 来源: 题型:
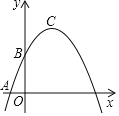
查看答案和解析>>【题目】在平面直角坐标系xOy中(如图).已知抛物线y=﹣
 x2+bx+c经过点A(﹣1,0)和点B(0,
x2+bx+c经过点A(﹣1,0)和点B(0, ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.(1)求这条抛物线的表达式;
(2)求线段CD的长;
(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
相关试题

