【题目】在平面直角坐标系xOy中,反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
(1)求反比例函数y1= ![]() 和一次函数y2=ax+b的表达式;
和一次函数y2=ax+b的表达式;
(2)点C 是坐标平面内一点,BC∥x 轴,AD⊥BC 交直线BC 于点D,连接AC.若AC= ![]() CD,求点C的坐标.
CD,求点C的坐标.
参考答案:
【答案】
(1)解:∵反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m),
的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m),
∴点A(1,3)在反比例函数y1= ![]() 的图象上,
的图象上,
∴k=1×3=3,
∴反比例函数的表达式为y1= ![]() .
.
∵点B(﹣3,m)在反比例函数y1= ![]() 的图象上,
的图象上,
∴m= ![]() =﹣1.
=﹣1.
∵点A(1,3)和点B(﹣3,﹣1)在一次函数y2=ax+b的图象上,
∴ ![]() ,解得:
,解得: ![]() .
.
∴一次函数的表达式为y2=x+2.
(2)解:依照题意画出图形,如图所示.
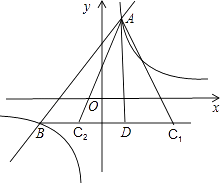
∵BC∥x轴,
∴点C的纵坐标为﹣1,
∵AD⊥BC于点D,
∴∠ADC=90°.
∵点A的坐标为(1,3),
∴点D的坐标为(1,﹣1),
∴AD=4,
∵在Rt△ADC中,AC2=AD2+CD2,且AC= ![]() CD,
CD,
∴ ![]() ,解得:CD=2.
,解得:CD=2.
∴点C1的坐标为(3,﹣1),点C2的坐标为(﹣1,﹣1).
故点C的坐标为(﹣1,﹣1)或(3,﹣1)
【解析】(1)把A点的坐标代入反比例函数解析式可求得k的值可得;再把B点的坐标代入已经求得的反比例函数解析式可求得m的值,再由A、B的坐标和待定系数法求得一次函数的解析式;
(2)易求出C点的纵坐标和点D的坐标,从而可得AD的长;在Rt△ADC中可求得CD的长,从而求出点C的坐标.
-
科目: 来源: 题型:
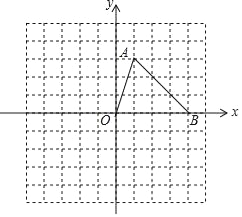
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABO的三个顶点坐标分别为A(1,3),B(4,0),O(0,0).
(1)画出将△ABO向左平移4个单位长度,再向上平移2个单位长度后得到的△A1B1O1;
(2)在(1)中,若△ABC上有一点M(3,1),则其在△A1B1O1中的对应点M1的坐标为 ;
(3)若将(1)中△A1B1O1看成是△ABO经过一次平移得到的,则这一平移的距离是 ;
(4)画出△ABO关于点O成中心对称的图形△A2B2O.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).
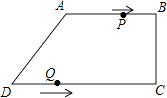
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若α、β为方程2x2﹣5x﹣1=0的两个实数根,则2α2+3αβ+5β的值为( )
A.﹣13
B.12
C.14
D.15 -
科目: 来源: 题型:
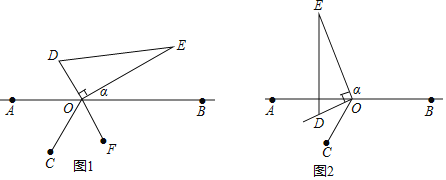
查看答案和解析>>【题目】如图1,点A、O、B在同一直线上,∠AOC=60°,在直线AB另一侧,直角三角形DOE绕直角顶点O逆时针旋转(当OD与OC重合时停止),设∠BOE=α:
(1)如图1,当DO的延长线OF平分∠BOC,∠α=______度;
(2)如图2,若(1)中直角三角形DOE继续逆时针旋转,当OD位于∠AOC的内部,且∠AOD=
 ∠AOC,∠α=__度;
∠AOC,∠α=__度;(3)在上述直角三角形DOE的旋转过程中,(∠COD+∠α)的度数是否改变?若不改变,请求出其度数;若改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O在直线AB上,∠AOC=30°,将一直角三角板的直角边OM与OA重合,ON在∠COB内部.现将三角板绕O沿顺时针方向以每秒2°的速度旋转,当ON与OB重合时停止转动.设运动时间为t(s).
(1)若直角边ON将∠COB分成∠CON:∠BON=3:2,求t的值;
(2)如图2,OG为三角板MON内部的射线,在旋转的过程中,OG始终平分∠MOB,请问∠AOM与∠NOG是否存在一定的数量关系?若存在,求出改数量关系;若不存在,请说明理由.
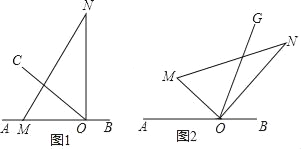
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AE是△ABC的外角∠CAD的平分线.
(1)若AE∥BC,如图1,试说明∠B=∠C;
(2)若AE交BC的延长线于点E,如图2,直接写出反应∠B、∠ACB、∠AEC之间关系的等式.

相关试题

