【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交与
轴分别交与![]() 、
、![]() 两点,
两点,![]() .
.
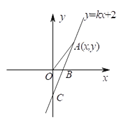
(![]() )写出
)写出![]() 点的坐标和
点的坐标和![]() 的值.
的值.
(![]() )若点
)若点![]() 是第一象限内的直线
是第一象限内的直线![]() 上的一个动点,当点
上的一个动点,当点![]() 运动过程中,试求出
运动过程中,试求出![]() 的面积
的面积![]() 与
与![]() 的函数关系式.
的函数关系式.
(![]() )在(
)在(![]() )的条件下:
)的条件下:
①当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积是
的面积是![]() .
.
②在①成立的情况下,![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 是等腰三角形.若存在,请写出满足条件的所有
是等腰三角形.若存在,请写出满足条件的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
参考答案:
【答案】(![]() )
)![]() ,
,![]() ;(
;(![]() )
)![]() ;(
;(![]() )①当
)①当![]() 时,
时,![]() 的面积为
的面积为![]() .②
.②![]() ,
,![]() ,
,![]() ,
,![]()
【解析】试题分析:(1)对于直线解析式,分别令x与y为0求出对应y与x的值,表示出OB与OC,根据已知等式确定出k的值,即可求出B的坐标;
(2)过A作AD垂直于x轴,可得AD为三角形AOB的高,根据三角形面积公式列出S与x的关系式即可;
(3)①令S=2,求出x的值,确定出A的坐标即可;
②在①成立的情况下,x轴上存在一点P,使△POA是等腰三角形,如图所示,分别求出P的坐标即可.
试题解析:
(![]() )令
)令![]() 中
中![]() ,
,
则![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
代入得![]() ,
,![]() .
.
(![]() )作
)作![]() 轴于
轴于![]()
∴![]() .
.
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(![]() )①由已知可得
)①由已知可得![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 的面积是
的面积是![]() .
.
②∵![]()
∴![]() .
.
∵![]() 为等腰
为等腰![]() .
.
若![]() ,则以
,则以![]() 为圆心,
为圆心,![]() 为半径画圆,交
为半径画圆,交![]() 轴于
轴于![]() ,
,
∴![]() ,
,
若![]() ,则以
,则以![]() 为圆心,
为圆心,![]() 为半径画圆,交
为半径画圆,交![]() 轴于
轴于![]() ,
,![]() ,
,
∴![]() ,
,![]()
若![]() ,则作
,则作![]() 的垂直平分线,交
的垂直平分线,交![]() 轴于
轴于![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
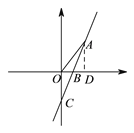
查看答案和解析>>【题目】如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接2008年北京奥运会,某学校组织了一次野外长跑活动,参加长跑的同学出发后,另一些同学从同地骑自行车前去加油助威。如图,线段L1,L2分别表示长跑的同学和骑自行车的同学行进的路程y(千米)随时间x(分钟)变化的函数图象.根据图象,解答下列问题:
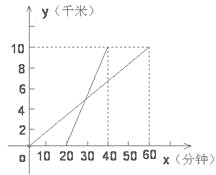
(1)分别求出长跑的同学和骑自行车的同学的行进路程y与时间x的函数表达式;
(2)求长跑的同学出发多少时间后,骑自行车的同学就追上了长跑的同学?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂计划生产A,B两款校服共500件,这两款校服的成本、售价如表所示:
 价格
价格类别
成本(元/件)
售价(元/件)
A款
30
45
B款
50
70
(1)求校服厂家销售完这批校服时所获得的利润y(元)与A款校服的生产数量x(件)之间的函数关系.
(2)若厂家计划B款校服的生产数量不超过A款校服的生产数量的4倍,应怎样安排生产才能使校服厂家在销售完这批校服时获得利润最多?此时获得利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知开始输入的x的值为正整数.若最后输出的结果为144,则满足条件的x的值为________;若经过一次运算就能输出结果,则x的最小值为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校组织初一同学春游,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座大客车,则多出一辆,且其余客车恰好坐满.已知45座客车日租金为每辆220元,60座大客车日租金为每辆300元.
求:(1)初一年级学生有多少人? 原计划租用45座客车多少辆?
(2)要使每个学生都有座位,怎样租用更合算?最低租金是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简下列多项式:
(1)
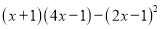
(2)
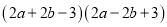
(3)若
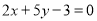 ,求
,求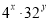 的值.
的值.(4)先化简,再求值:(2x﹣1)2﹣(3x+1)(3x﹣1)+5x(x﹣1),其中x=﹣2.
相关试题

