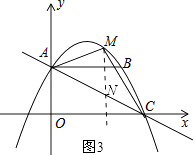
【题目】如图,平面直角坐标系xOy中,直线AC分别交坐标轴于A,C(8,0)两点,AB∥x轴,B(6,4).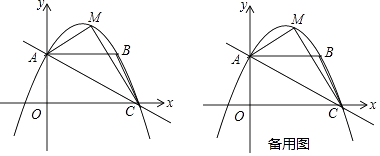
(1)求过B,C两点的抛物线y=ax2+bx+4的表达式;
(2)点P从C点出发以每秒1个单位的速度沿线段CO向O点运动,同时点Q从A点出发以相同的速度沿线段AB向B点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为t秒.当t为何值时,四边形BCPQ为平行四边形;
(3)若点M为直线AC上方的抛物线上一动点,当点M运动到什么位置时,△AMC的面积最大?求出此时M点的坐标和△AMC的最大面积.
参考答案:
【答案】
(1)
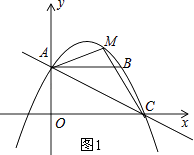
解:如图1,
∵过B(6,4),C(8,0)两点的抛物线y=ax2+bx+4.
∴ ![]() ,
,
解得 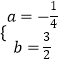 .
.
∴过B、C三点的抛物线的表达式为y=﹣ ![]() x2+
x2+ ![]() x+4
x+4
(2)
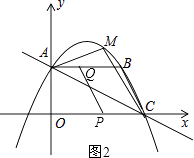
解:如图2,
由题可得:BQ=6﹣t,CP=t.
当BQ∥CP且BQ=CP时,四边形BCPQ为平行四边形.
∴6﹣t=t.
解得:t=3.
(3)
解:过点M作x轴的垂线,交AC于点N,如图3,
设直线AC的解析式为y=kx+4,
则有8k+4=0.
解得:k=﹣ ![]() .
.
∴直线AC的解析式为y=﹣ ![]() x+4.
x+4.
设点M的横坐标为m,
则有yM=﹣ ![]() m2+
m2+ ![]() m+4,yN=﹣
m+4,yN=﹣ ![]() m+4.
m+4.
∴MN=yM﹣yN
=(﹣ ![]() m2+
m2+ ![]() m+4)﹣(﹣
m+4)﹣(﹣ ![]() m+4)
m+4)
=﹣ ![]() m2+2m.
m2+2m.
∴S△AMC=S△AMN+S△CMN
= ![]() MNOC
MNOC
= ![]() ×(﹣
×(﹣ ![]() m2+2m)×8
m2+2m)×8
=﹣m2+8m
=﹣(m﹣4)2+16.(0<m<8)
∵﹣1<0,
∴当m=4时,S△AMC取到最大值,最大值为16,此时点M的坐标为(4,6).
【解析】(1)用待定系数法就可求出过B,C三点的抛物线的表达式.(2)若四边形BCPQ为平行四边形,则有BQ=CP,从而建立关于t的方程,就可求出t的值.(3)过点M作x轴的垂线,交AC于点N,设点M的横坐标为m,由S△AMC=S△AMN+S△CMN= ![]() MNOC可以得到S△AMC=﹣(m﹣4)2+16.然后利用二次函数的最值性就可解决问题
MNOC可以得到S△AMC=﹣(m﹣4)2+16.然后利用二次函数的最值性就可解决问题
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )
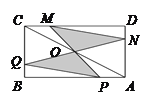
A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读新知:移项且合并同类项之后,只含有偶次项的四次方程称作双二次方程.其一般形式为ax4+bx2+c=0(a≠0),一般通过换元法解之,具体解法是设 x2=y,则原四次方程化为一元二次方程:ay2+by+c=0,解出y之后代入x2=y,从而求出x的值.例如解:4x4﹣8y2+3=0
解:设x2=y,则原方程可化为:4y2﹣8y+3=0
∵a=4,b=﹣8,c=3
∴b2﹣4ac=﹣(﹣8)2﹣4×4×3=16>0
∴y=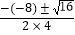 =
= 
∴y1= ,
,
∴y2=
∴当y1= 时,x2=
时,x2= 
∴x1= ,x2=﹣
,x2=﹣  ;当y1=
;当y1=  时,x2=
时,x2= 
∴x3=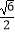 ,x4=﹣
,x4=﹣ 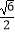
小试牛刀:请你解双二次方程:x4﹣2x2﹣8=0
归纳提高:思考以上解题方法,试判断双二次方程的根的情况,下列说法正确的是(选出所有的正确答案)
①当b2﹣4ac≥0时,原方程一定有实数根;②当b2﹣4ac<0时,原方程一定没有实数根;③当b2﹣4ac≥0,并且换元之后的一元二次方程有两个正实数根时,原方程有4个实数根,换元之后的一元二次方程有一个正实数根一个负实数根时,原方程有2个实数根;④原方程无实数根时,一定有b2﹣4ac<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,∠MON=80,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P. 试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式,不能因式分解的是( )
A. m2+4m+4 B. x2+y2 C. a2﹣2ab+b2 D. a2﹣b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】2011年淮安市人均GDP约为35200元,35200用科学记数法表示为
-
科目: 来源: 题型:
查看答案和解析>>【题目】选择适当的方法解方程:
(1)2(x﹣3)=3x(x﹣3).
(2)2x2﹣3x+1=0.
相关试题

