【题目】如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则BG的长是 . 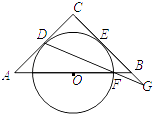
参考答案:
【答案】2 ![]() ﹣2
﹣2
【解析】解:连接OD.
∵AC为圆O的切线,∴OD⊥AC,
又∵AC=BC=4,∠C=90°,
∴∠A=45°,
根据勾股定理得:AB= ![]() =4
=4 ![]() ,
,
又∵O为AB的中点,
∴AO=BO= ![]() AB=2
AB=2 ![]() ,
,
∴圆的半径DO=FO=AOsinA=2 ![]() ×
× ![]() =2,
=2,
∴BF=OB﹣OF=2 ![]() ﹣2.
﹣2.
∵GC⊥AC,OD⊥AC,
∴OD∥CG,
∴∠ODF=∠G,
又∵∠OFD=∠BFG,
∴△ODF∽△BGF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴BG=2 ![]() ﹣2.
﹣2.
所以答案是:2 ![]() ﹣2.
﹣2.
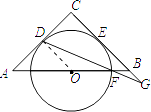
【考点精析】关于本题考查的切线的性质定理和相似三角形的判定与性质,需要了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为( )

A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】补全解题过程.
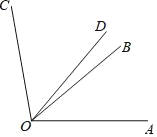
已知:如图,∠AOB=40°,∠BOC=60°,OD平分∠AOC.求∠BOD的度数.
解:∵∠AOC=∠AOB+∠ ,
又∵∠AOB=40°,∠BOC=60°,
∴∠AOC= °.
∵OD平分∠AOC,
∴∠AOD= ∠AOC( ).
∴∠AOD=50°.
∴∠BOD=∠AOD﹣∠ .
∴∠BOD= °.
-
科目: 来源: 题型:
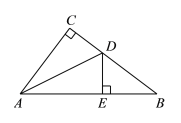
查看答案和解析>>【题目】如图,
 中,
中,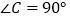 ,
,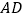 平分
平分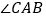 交
交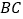 于点
于点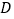 ,
,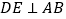 于点
于点 ,如果
,如果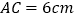 ,
,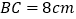 ,那么
,那么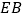 的长为________
的长为________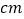 ,
,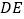 的长为_______
的长为_______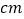 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC绕点B逆时针旋转到△A′BC′,使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着北京申办冬奥会的成功,愈来愈多的同学开始关注我国的冰雪体育项目. 小健从新闻中了解到:在2018年平昌冬奥会的短道速滑男子500米决赛中,中国选手武大靖以39秒584的成绩打破世界纪录,收获中国男子短道速滑队在冬奥会上的首枚金牌. 同年11月12日,武大靖又以39秒505的成绩再破世界纪录. 于是小健对同学们说:“2022年北京冬奥会上武大靖再获金牌的可能性大小是
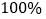 .”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
.”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,同学们经历了摸球的实例分析和计算过程后,对求简单随机事件发生的可能性大小的计算方法和步骤进行了归纳. 请你将下列求简单随机事件发生的可能性大小的计算方法和步骤的正确顺序写出来___________.(填写序号即可)
①确定所有可能发生的结果个数
 和其中出现所求事件的结果个数
和其中出现所求事件的结果个数
②计算所求事件发生的可能性大小,即
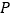 (所求事件)
(所求事件)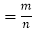
③列出所有可能发生的结果,并判断每个结果发生的可能性都相等
相关试题

