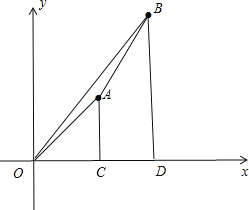
【题目】在平面直角坐标系中,o为坐标原点,点A的坐标为(![]() ,3),点B的坐标(
,3),点B的坐标(![]() ,6).
,6).
(1)若AB与坐标轴平行,求AB的长;
(2)若![]() 满足
满足![]() AC⊥
AC⊥![]() 轴,垂足为C,BD⊥
轴,垂足为C,BD⊥![]() 轴,垂足为D:
轴,垂足为D:
①求四边形ACDB的面积;
②连AB、OA、OB,若△OAB的面积大于6而小于10,求![]() 的取值范围。
的取值范围。
参考答案:
【答案】(1)AB=3;(2)①9;②6<a<![]() 或﹣
或﹣![]() <a<﹣2
<a<﹣2
【解析】
(1)分析题意可知,AB与y轴平行,则AB的长为两点的纵坐标之差;
(2)①先解方程组得到b﹣a=2,则根据梯形的面积公式可计算出四边形ACDB的面积为9;
②分类讨论:当a>0,S△OAB=S△OBD﹣S△OAC﹣S梯形ACDB=![]() a﹣3,则6<
a﹣3,则6<![]() a﹣3<10,解得6<a<
a﹣3<10,解得6<a<![]() ;当a<0,b>0,S△OAB=S梯形ACDB﹣S△OBD﹣S△OAC=3﹣
;当a<0,b>0,S△OAB=S梯形ACDB﹣S△OBD﹣S△OAC=3﹣![]() a,则6<3﹣
a,则6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,而b=2+a>0,则a>﹣2,故舍去;当a<0,b<0,S△OAB=S△OBD+S梯形ACDB﹣S△OAC=3﹣
<a<﹣2,而b=2+a>0,则a>﹣2,故舍去;当a<0,b<0,S△OAB=S△OBD+S梯形ACDB﹣S△OAC=3﹣![]() a,则6<3﹣
a,则6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,于是得到a的取值范围为6<a<
<a<﹣2,于是得到a的取值范围为6<a<![]() 或﹣
或﹣![]() <a<﹣2.
<a<﹣2.
(1)∵AB与坐标轴平行,即AB平行于y轴,
∴AB=6﹣3=3;
(2)①由方程组![]() 得b﹣a=2,
得b﹣a=2,
∵AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,
∴C(a,0),D(b,0),如图,
∴四边形ACDB的面积=![]() (3+6)(b﹣a)=
(3+6)(b﹣a)=![]() 92=9;
92=9;
②当a>0,
∵S△OAB=S△OBD﹣S△OAC﹣S梯形ACDB,
∴S△OAB=![]() 6b﹣
6b﹣![]() 3a﹣9=3b﹣
3a﹣9=3b﹣![]() a﹣9,
a﹣9,
而b=2+a,
∴S△OAB=3(2+a)﹣![]() a﹣9=
a﹣9=![]() a﹣3,
a﹣3,
∴6<![]() a﹣3<10,解得6<a<
a﹣3<10,解得6<a<![]() ;
;
当a<0,b>0,
S△OAB=S梯形ACDB﹣S△OBD﹣S△OAC=9﹣![]() 6b+
6b+![]() 3a=9﹣3b+
3a=9﹣3b+![]() a=9﹣3(2+a)+
a=9﹣3(2+a)+![]() a=3﹣
a=3﹣![]() a
a
∴6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,
<a<﹣2,
而b=2+a>0,则a>﹣2,故舍去,
当a<0,b<0,
∵S△OAB=S△OBD+S梯形ACDB﹣S△OAC=﹣![]() 6b+9+
6b+9+![]() 3a=﹣3b+9+
3a=﹣3b+9+![]() a=﹣3(2+a)+9+
a=﹣3(2+a)+9+![]() a=3﹣
a=3﹣![]() a
a
∴6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,
<a<﹣2,
综上所述,a的取值范围为6<a<![]() 或﹣
或﹣![]() <a<﹣2.
<a<﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 平分
平分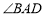 交
交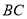 于点
于点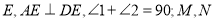 分别是
分别是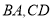 延长线上的点,
延长线上的点,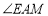 和
和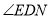 的平分线交于点
的平分线交于点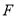 .下列结论:①
.下列结论:①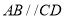 ;②
;②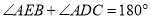 ;③
;③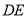 平分
平分 ;④
;④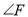 为定值.其中结论正确的有_______(填写所有正确的序号).
为定值.其中结论正确的有_______(填写所有正确的序号).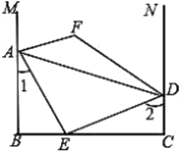
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=100°,AC=AE,BC=BD,则∠DCE的度数为

A. 20° B. 25° C. 30° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=
 AB中,一定正确的是( )
AB中,一定正确的是( )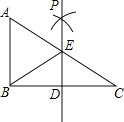
A.①②③ B.①②④ C.①③④ D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )

A.
 B.
B.  C. 5 D.
C. 5 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑到学校.如果小明跑步的速度均匀的,到达小彬家用了8分钟,整个跑步过程用时共32分钟.
(1)以小明家为原点、向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家;
(2)用点C表示出学校的位置;
(3)求小彬家与学校之间的距离.

相关试题

