【题目】如图,![]() 平分
平分![]() 交
交![]() 于点
于点![]() 分别是
分别是![]() 延长线上的点,
延长线上的点,![]() 和
和![]() 的平分线交于点
的平分线交于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 为定值.其中结论正确的有_______(填写所有正确的序号).
为定值.其中结论正确的有_______(填写所有正确的序号).
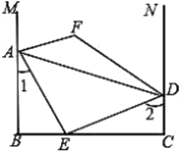
参考答案:
【答案】①③④
【解析】
先根据AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,∠EAM和∠EDN的平分线交于点F,由三角形内角和定理以及平行线的性质即可得出结论.
解:∵AB⊥BC,AE⊥DE,
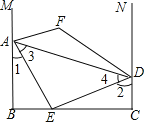
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°-90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=![]() ×270°=135°.
×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°-90°=45°,
∴∠F=180°-(∠FAD+∠FDA)=180-45°=135°,故④正确.
故答案为:①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已如点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2019个单位长度没有弹性的细线(线的相细忽略不计)的一端固定在A处,并按
 的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.
的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别
平均数
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的平分线BE交AD于点F,则图中共有等腰三角形( )
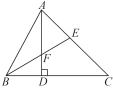
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=100°,AC=AE,BC=BD,则∠DCE的度数为

A. 20° B. 25° C. 30° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=
 AB中,一定正确的是( )
AB中,一定正确的是( )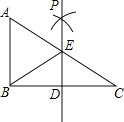
A.①②③ B.①②④ C.①③④ D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,o为坐标原点,点A的坐标为(
 ,3),点B的坐标(
,3),点B的坐标( ,6).
,6).(1)若AB与坐标轴平行,求AB的长;
(2)若
 满足
满足 AC⊥
AC⊥ 轴,垂足为C,BD⊥
轴,垂足为C,BD⊥ 轴,垂足为D:
轴,垂足为D:①求四边形ACDB的面积;
②连AB、OA、OB,若△OAB的面积大于6而小于10,求
 的取值范围。
的取值范围。
相关试题

