【题目】如图1,在平面直角坐标系xOy中,线段AB在x轴的正半轴上移动,且AB=1,过点A、B作y轴的平行线分别交函数y1=![]() (x>0)与y2=
(x>0)与y2=![]() (x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).
(x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).
(1)连接OC、OE,则△OCE面积为 ;
(2)连接CF,当m为何值时,四边形ABFC是矩形;
(3)连接CD、EF,判断四边形CDFE能否是平行四边形,并说明理由;
(4)如图2,经过点B和y轴上点G(0,4)作直线BG交直线AC于点H,若点H的纵坐标为正整数,请求出整数m的值.

参考答案:
【答案】(1)1;(2)![]() ;(3)不能;(4)m=1或3
;(3)不能;(4)m=1或3
【解析】
(1)先表示出点C,E坐标,再用三角形面积公式即可得出结论;
(2)先表示出点C,F坐标,利用矩形的性质对边相等建立方程求解即可得出结论;
(3)先表示出点C,D,E,F的坐标,进而求出CE,DF,判断出CE≠DF,即可得出结论;
(4)先求出直线BG的解析式,进而表示出点H的坐标,最后用![]() 是正整数,建立方程即可得出结论.
是正整数,建立方程即可得出结论.
(1)∵点A的横坐标为m,且AC∥y轴,
∴C(m,![]() ,E(m,
,E(m,![]() ),
),
∴S△COE=![]() CE×OA=
CE×OA=![]() (
(![]() ﹣
﹣![]() )m=1,
)m=1,
故答案为:1;
(2)若四边形ABFC是矩形,则 AC=BF,
∵AB=1,点A的横坐标为m,
∴点B的横坐标为:m+1
∴C(m,![]() ),F(m+1,
),F(m+1,![]() ),
),
∴AC=![]() ,FB=
,FB=![]() ,
,
∴![]() =
=![]() ,
,
∴m=![]() ;
;
(3)不能,
理由:由题意得,C(m,![]() ),E(m,
),E(m,![]() ),D(m+1,
),D(m+1,![]() ,F(m+1,
,F(m+1,![]() ),
),
∴CE=![]() ﹣
﹣![]() =
=![]() ,DF=
,DF=![]() ﹣
﹣![]() =
=![]() ,
,
∴CE≠DF,
∵CE∥DF,
∴四边形CDFE不是平行四边形;
(4)∵G(0,4),
∴设直线BG的表达式为y=kx+4(k≠0),
将B(m+1,0)代入y=kx+4中得k(m+1)+4=0,
∴k=﹣![]() ,
,
∴直线BG的解析式为y=﹣![]() x+4,
x+4,
将x=m代入y=﹣![]() x+4中得y=﹣
x+4中得y=﹣![]() x+4=
x+4=![]() ,
,
∴点H(m,![]() ),
),
∵m>0,
∴m+1>1,
∵点H的纵坐标是正整数,
∴m+1=2或m+1=4,
∴m=1或3.
-
科目: 来源: 题型:
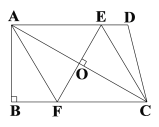
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=6,BC=8,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:数学课上,老师展示了一位同学的作业如下:
已知多项式
 ,
, ,
,
(1)求
 ;
;(2)若
 的结果与字母
的结果与字母 的取值无关,求
的取值无关,求 的值.
的值.下面是这位同学第(1)问的解题过程:
解:(1)
 …………………………第一步
…………………………第一步 …………………………………………………第二步
…………………………………………………第二步 ……………………………………………………………第三步
……………………………………………………………第三步回答问题:
(i)这位同学第______步开始出现错误,错误原因是____________;
(ii)请你帮这位同学完成题目中的第(2)问.
-
科目: 来源: 题型:
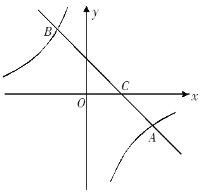
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y =ax+b的图像与反比例函数y =
 的图像交于A(4,﹣2)、B(﹣2,m)两点,与x轴交于点C.
的图像交于A(4,﹣2)、B(﹣2,m)两点,与x轴交于点C.(1)求a,m的值;
(2)请直接写出不等式ax+b≥
 的解集;
的解集;(3)点P在反比例函数图像上,且点P的横坐标为-4,在平面直角坐标系中是否存在一点Q,使得以A、B、P、Q为顶点的四边形为平行四边形?如果存在,请直接写出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种产品,每件产品的成本为2400元,销售单价定位3000元,该商场为了促销,规定客户一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元;
(1)设一次购买这种产品x(x≥10)件,商场所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(2)在客户购买产品的件数尽可能少的前提下,商场所获的利润为12000元,此时该商场销售了多少件产品?
(3)填空:该商场的销售人员发现,当客户一次购买产品的件数在某一个区间时,会出现随着一次购买的数量的增多,商场所获的利润反而减少这一情况,客户一次购买产品的数量x满足的条件是 (其它销售条件不变)
-
科目: 来源: 题型:
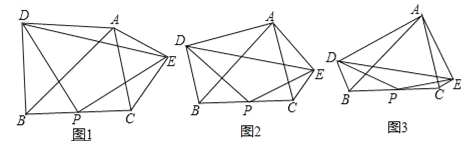
查看答案和解析>>【题目】已知在△ABC中,∠BAC=60°,点P为边BC的中点,分别以AB和AC为斜边向外作Rt△ABD和Rt△ACE,且∠DAB=∠EAC=α,连结PD,PE,DE.
(1)如图1,若α=45°,则
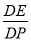 = ;
= ;(2)如图2,若α为任意角度,求证:∠PDE=α;
(3)如图3,若α=15°,AB=8,AC=6,则△PDE的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填写下表,并观察下列两个代数式的值的变化情况。

(2)随着n的值逐渐变大,两个代数式的值如何变化?
(3)估计一下,哪个代数式的值先超过100?
相关试题

