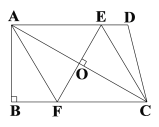
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=6,BC=8,求EF的长.
参考答案:
【答案】(1)详见解析;(2)![]()
【解析】
(1)由于知道了EF垂直平分AC,因此只要证出四边形AFCE是平行四边形即可得出AFCE是菱形的结论.
(2)根据勾股定理得出AC,进而利用勾股定理解答即可.
证明:(1)∵EF是对角线AC的垂直平分线,
∴AO=CO,AC⊥EF,
∵AD∥BC,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
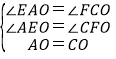 ,
,
∴△AEO≌△CFO(AAS),
∴AE=CF,
∴四边形AFCE是平行四边形,
又∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵∠B=90°,AB=6,BC=8,
∴AC= ![]() ,
,
∵四边形AFCE是菱形,
∴AF=FC,
在Rt△ABF中,设AF=FC=x,则BF=8-x
∴AB2+BF2=AF2,
∴62+(8-x)2=x2,
∴x=![]() ,
,
∴OF ![]() ,
,
∴EF=2OF=![]() .
.
-
科目: 来源: 题型:
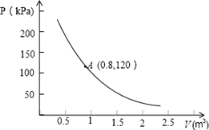
查看答案和解析>>【题目】某气球内充满了一定量的气体,当温度不变时,气球内气体的压强P(kPa)是气体体积V(m3)的反比例函数,其图像如图所示.
(1)求这一函数的表达式;
(2)当气体压强为48kPa时,求V的值?
(3)当气球内的体积小于0.6m3时,气球将爆炸,为了安全起见,气体的压强不大于多少?
-
科目: 来源: 题型:
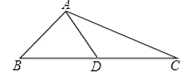
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AC=13,边BC上的中线AD=6.
(1)以点D为对称中心,作出△ABD的中心对称图形;
(2)求点A到BC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)按要求将下列几何体进行分类,并将分类后几何体的名称写在对应的括号内.

柱体:{ …}
锥体:{ …}
(2)6个完全相同的正方体组成如图所示的几何体,画出该几何体从正面,左面看到的形状图(用阴影画在所给的方格中)
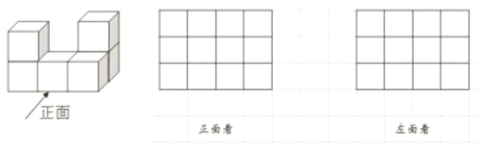
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:数学课上,老师展示了一位同学的作业如下:
已知多项式
 ,
, ,
,
(1)求
 ;
;(2)若
 的结果与字母
的结果与字母 的取值无关,求
的取值无关,求 的值.
的值.下面是这位同学第(1)问的解题过程:
解:(1)
 …………………………第一步
…………………………第一步 …………………………………………………第二步
…………………………………………………第二步 ……………………………………………………………第三步
……………………………………………………………第三步回答问题:
(i)这位同学第______步开始出现错误,错误原因是____________;
(ii)请你帮这位同学完成题目中的第(2)问.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y =ax+b的图像与反比例函数y =
 的图像交于A(4,﹣2)、B(﹣2,m)两点,与x轴交于点C.
的图像交于A(4,﹣2)、B(﹣2,m)两点,与x轴交于点C.(1)求a,m的值;
(2)请直接写出不等式ax+b≥
 的解集;
的解集;(3)点P在反比例函数图像上,且点P的横坐标为-4,在平面直角坐标系中是否存在一点Q,使得以A、B、P、Q为顶点的四边形为平行四边形?如果存在,请直接写出点Q的坐标.
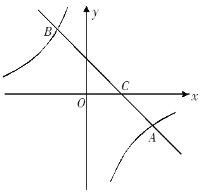
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,线段AB在x轴的正半轴上移动,且AB=1,过点A、B作y轴的平行线分别交函数y1=
 (x>0)与y2=
(x>0)与y2=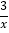 (x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).
(x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).(1)连接OC、OE,则△OCE面积为 ;
(2)连接CF,当m为何值时,四边形ABFC是矩形;
(3)连接CD、EF,判断四边形CDFE能否是平行四边形,并说明理由;
(4)如图2,经过点B和y轴上点G(0,4)作直线BG交直线AC于点H,若点H的纵坐标为正整数,请求出整数m的值.

相关试题

