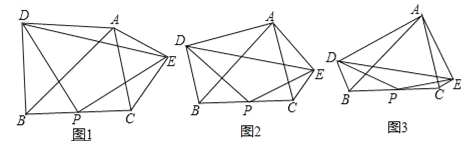
【题目】已知在△ABC中,∠BAC=60°,点P为边BC的中点,分别以AB和AC为斜边向外作Rt△ABD和Rt△ACE,且∠DAB=∠EAC=α,连结PD,PE,DE.
(1)如图1,若α=45°,则![]() = ;
= ;
(2)如图2,若α为任意角度,求证:∠PDE=α;
(3)如图3,若α=15°,AB=8,AC=6,则△PDE的面积为 .
参考答案:
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1) 分别取AB、AC中点F、G,连接DF、PF、PG、EG,证明AFPG为平行四边形,再证明△DFP和△PGE全等,再证明∠DPE=90°,最后得到△DEP是等腰直角三角形.
(2)类似(1)证明四边形AFPG为平行四边形,证明△DFP和△PGE全等,再证明∠DPE=180°﹣∠DFB,∠DFA=180°﹣∠DFB,所以∠DPE=∠DFA,所以等腰三角形DPE和等腰三角形ADF中,∠PDE=∠DAF=α.
(3)同理(1)求出DP=EP长度,由(2)可得,∠PDE=α=15°=∠PED,过点E作DP的垂线,交DP的延长线于H,则∠EPH=30°,所以可求得EH= ![]() PE=
PE= ![]() ,所以可以得到△PDE的面积.
,所以可以得到△PDE的面积.
试题分析:
解:(1)分别取AB、AC中点F、G,连接DF、PF、PG、EG,则根据三角形中位线定理可得,AF=PG,AG=PF,即四边形AFPG为平行四边形,
∴∠PFB=∠BAC=∠PGC=60°,∵Rt△ABD和Rt△ACE中,∠DAB=∠EAC=α=45°,
∴△ABD和△ACE都是等腰直角三角形,∴DF⊥AB,EG⊥AC,且DF=AF=PG,PF=AG=EG,∴∠DFP=∠PGE=150°,
在△DFP和△PGE中, 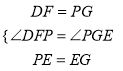 ,
,
∴△DFP≌△PGE(SAS),
∴DP=PE,∠GPE=∠FDP,
∵△DPF中,∠FDP+∠DPF+∠PFB=90°,而∠PFB=∠FPG,
∴∠GPE+∠DPF+∠FPG=90°,即∠DPE=90°,
∴△DEP是等腰直角三角形,∴![]() .
.
(2)证明:分别取AB、AC中点F、G,连接DF、PF、PG、EG,则根据三角形中位线定理可得,AF=PG,AG=PF,即四边形AFPG为平行四边形,
∴∠PFB=∠BAC=∠PGC=60°,∵Rt△ABD和Rt△ACE中,DF=AF,GE=AG,∴DF=PG,PF=EG,∠DFB=2∠DAF=2α,∠EGC=2∠CAE=2α,
∴∠DFP=∠PGE,在△DFP和△PGE中, 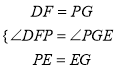 ,
,
∴△DFP≌△PGE(SAS),∴DP=PE,∠GPE=∠FDP,
∵在△DFP中,∠FDP+∠DPF+∠PFB=180°﹣∠DFB,而∠PFB=∠FPG,∴∠GPE+∠DPF+∠FPG=180°﹣∠DFB,即∠DPE=180°﹣∠DFB,
又∵∠DFA=180°﹣∠DFB,∴∠DPE=∠DFA,
∴在等腰三角形DPE和等腰三角形ADF中,∠PDE=∠DAF=α.
(3)分别取AB、AC中点F、G,连接DF、PF、PG、EG,则根据三角形中位线定理可得,AF=PG=4,AG=PF=3,即四边形AFPG为平行四边形,∴∠PFB=∠BAC=∠PGC=60°,
∵Rt△ABD和Rt△ACE中,DF=AF,GE=AG,∴DF=PG=4,PF=EG=3,∠DFB=2∠DAF=2α=30°,∠EGC=2∠CAE=2α=30°,∴∠DFP=∠PGE=90°,
∴DP=EP= ![]() =5,
=5,
由(2)可得,∠PDE=α=15°=∠PED,过点E作DP的垂线,交DP的延长线于H,则∠EPH=30°,∴EH= ![]() PE=
PE= ![]() ,∴△PDE的面积=
,∴△PDE的面积= ![]() ×DP×EH=
×DP×EH= ![]() ×5×
×5×![]() =
= ![]() .
.

-
科目: 来源: 题型:
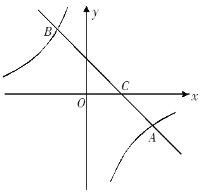
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y =ax+b的图像与反比例函数y =
 的图像交于A(4,﹣2)、B(﹣2,m)两点,与x轴交于点C.
的图像交于A(4,﹣2)、B(﹣2,m)两点,与x轴交于点C.(1)求a,m的值;
(2)请直接写出不等式ax+b≥
 的解集;
的解集;(3)点P在反比例函数图像上,且点P的横坐标为-4,在平面直角坐标系中是否存在一点Q,使得以A、B、P、Q为顶点的四边形为平行四边形?如果存在,请直接写出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,线段AB在x轴的正半轴上移动,且AB=1,过点A、B作y轴的平行线分别交函数y1=
 (x>0)与y2=
(x>0)与y2=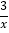 (x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).
(x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).(1)连接OC、OE,则△OCE面积为 ;
(2)连接CF,当m为何值时,四边形ABFC是矩形;
(3)连接CD、EF,判断四边形CDFE能否是平行四边形,并说明理由;
(4)如图2,经过点B和y轴上点G(0,4)作直线BG交直线AC于点H,若点H的纵坐标为正整数,请求出整数m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种产品,每件产品的成本为2400元,销售单价定位3000元,该商场为了促销,规定客户一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元;
(1)设一次购买这种产品x(x≥10)件,商场所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(2)在客户购买产品的件数尽可能少的前提下,商场所获的利润为12000元,此时该商场销售了多少件产品?
(3)填空:该商场的销售人员发现,当客户一次购买产品的件数在某一个区间时,会出现随着一次购买的数量的增多,商场所获的利润反而减少这一情况,客户一次购买产品的数量x满足的条件是 (其它销售条件不变)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填写下表,并观察下列两个代数式的值的变化情况。

(2)随着n的值逐渐变大,两个代数式的值如何变化?
(3)估计一下,哪个代数式的值先超过100?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=
 c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+ cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+
 cx+b=0必有实数根;
cx+b=0必有实数根;若x=1是“勾系一元二次方程”ax+
 cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是 ,求△ABC面积.
,求△ABC面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以
 ,
,  ,
,  的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以
 ,
,  ,
,  的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形其中所有正确结论的序号为______.
相关试题

