【题目】阅读材料:数学课上,老师展示了一位同学的作业如下:
已知多项式![]() ,
,![]() ,
,![]()
(1)求![]() ;
;
(2)若![]() 的结果与字母
的结果与字母![]() 的取值无关,求
的取值无关,求![]() 的值.
的值.
下面是这位同学第(1)问的解题过程:
解:(1)![]() …………………………第一步
…………………………第一步
![]() …………………………………………………第二步
…………………………………………………第二步
![]() ……………………………………………………………第三步
……………………………………………………………第三步
回答问题:
(i)这位同学第______步开始出现错误,错误原因是____________;
(ii)请你帮这位同学完成题目中的第(2)问.
参考答案:
【答案】(i)二;去括号时,括号前面是负号,去掉括号和负号,括号了的每一项要变号;(ii)![]() .
.
【解析】
根据整式的混合运算法则,先把A,B代入等式,再进行计算,去括号,合并同类项,即可解答.
解:(i)二
去括号时,括号前面是负号,去掉括号和负号,括号了的每一项要变号.
(ii)![]()
![]()
![]()
![]()
因为![]() 的结果与字母
的结果与字母![]() 的取值无关,
的取值无关,
所以![]() ,
,
![]() .
.
-
科目: 来源: 题型:
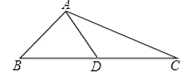
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AC=13,边BC上的中线AD=6.
(1)以点D为对称中心,作出△ABD的中心对称图形;
(2)求点A到BC的距离.
-
科目: 来源: 题型:
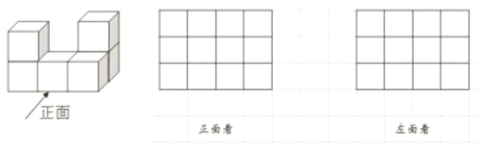
查看答案和解析>>【题目】(1)按要求将下列几何体进行分类,并将分类后几何体的名称写在对应的括号内.

柱体:{ …}
锥体:{ …}
(2)6个完全相同的正方体组成如图所示的几何体,画出该几何体从正面,左面看到的形状图(用阴影画在所给的方格中)
-
科目: 来源: 题型:
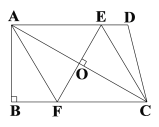
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=6,BC=8,求EF的长.
-
科目: 来源: 题型:
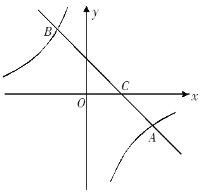
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y =ax+b的图像与反比例函数y =
 的图像交于A(4,﹣2)、B(﹣2,m)两点,与x轴交于点C.
的图像交于A(4,﹣2)、B(﹣2,m)两点,与x轴交于点C.(1)求a,m的值;
(2)请直接写出不等式ax+b≥
 的解集;
的解集;(3)点P在反比例函数图像上,且点P的横坐标为-4,在平面直角坐标系中是否存在一点Q,使得以A、B、P、Q为顶点的四边形为平行四边形?如果存在,请直接写出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,线段AB在x轴的正半轴上移动,且AB=1,过点A、B作y轴的平行线分别交函数y1=
 (x>0)与y2=
(x>0)与y2=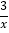 (x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).
(x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).(1)连接OC、OE,则△OCE面积为 ;
(2)连接CF,当m为何值时,四边形ABFC是矩形;
(3)连接CD、EF,判断四边形CDFE能否是平行四边形,并说明理由;
(4)如图2,经过点B和y轴上点G(0,4)作直线BG交直线AC于点H,若点H的纵坐标为正整数,请求出整数m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种产品,每件产品的成本为2400元,销售单价定位3000元,该商场为了促销,规定客户一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元;
(1)设一次购买这种产品x(x≥10)件,商场所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(2)在客户购买产品的件数尽可能少的前提下,商场所获的利润为12000元,此时该商场销售了多少件产品?
(3)填空:该商场的销售人员发现,当客户一次购买产品的件数在某一个区间时,会出现随着一次购买的数量的增多,商场所获的利润反而减少这一情况,客户一次购买产品的数量x满足的条件是 (其它销售条件不变)
相关试题

