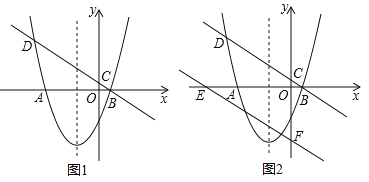
【题目】如图1,抛物线y=ax2+2x+c与x轴交于A(﹣4,0),B(1,0)两点,过点B的直线y=kx+![]() 分别与y轴及抛物线交于点C,D.
分别与y轴及抛物线交于点C,D.
(1)求直线和抛物线的表达式;
(2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;
(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线解析式为:y=![]() ,BD解析式为y=﹣
,BD解析式为y=﹣![]() ;(2)t的值为
;(2)t的值为![]() 、
、![]() 、
、![]() .(3)N点坐标为(﹣2,﹣2),M点坐标为(﹣
.(3)N点坐标为(﹣2,﹣2),M点坐标为(﹣![]() ,﹣
,﹣![]() ),
),![]() .
.
【解析】(1)利用待定系数法求解可得;
(2)先求得点D的坐标,过点D分别作DE⊥x轴、DF⊥y轴,分P1D⊥P1C、P2D⊥DC、P3C⊥DC三种情况,利用相似三角形的性质逐一求解可得;
(3)通过作对称点,将折线转化成两点间距离,应用两点之间线段最短.
(1)把A(﹣4,0),B(1,0)代入y=ax2+2x+c,
得![]() ,
,
解得: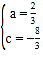 ,
,
∴抛物线解析式为:y=![]() ,
,
∵过点B的直线y=kx+![]() ,
,
∴代入(1,0),得:k=﹣![]() ,
,
∴BD解析式为y=﹣![]() ;
;
(2)由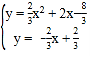 得交点坐标为D(﹣5,4),
得交点坐标为D(﹣5,4),
如图1,过D作DE⊥x轴于点E,作DF⊥y轴于点F,
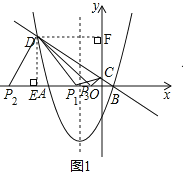
当P1D⊥P1C时,△P1DC为直角三角形,
则△DEP1∽△P1OC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得t=![]() ,
,
当P2D⊥DC于点D时,△P2DC为直角三角形
由△P2DB∽△DEB得![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得:t=![]() ;
;
当P3C⊥DC时,△DFC∽△COP3,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:t=![]() ,
,
∴t的值为![]() 、
、![]() 、
、![]() .
.
(3)由已知直线EF解析式为:y=﹣![]() x﹣
x﹣![]() ,
,
在抛物线上取点D的对称点D′,过点D′作D′N⊥EF于点N,交抛物线对称轴于点M
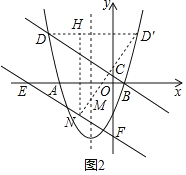
过点N作NH⊥DD′于点H,此时,DM+MN=D′N最小.
则△EOF∽△NHD′
设点N坐标为(a,﹣![]() ),
),
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:a=﹣2,
则N点坐标为(﹣2,﹣2),
求得直线ND′的解析式为y=![]() x+1,
x+1,
当x=﹣![]() 时,y=﹣
时,y=﹣![]() ,
,
∴M点坐标为(﹣![]() ,﹣
,﹣![]() ),
),
此时,DM+MN的值最小为![]() =
=![]() =2
=2![]() .
.
-
科目: 来源: 题型:
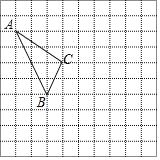
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;并写出B点坐标;
(2)请作出△ABC关于y轴对称的△A'B'C';
(3)请作出将△ABC向下平移的3个单位,再向右平移5个单位后的△A1B1C1;则点A1的坐标为_____;点B1的坐标为______,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.
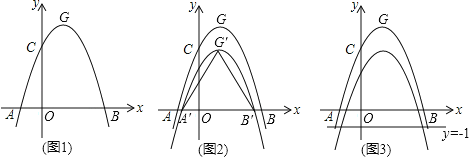
(1)求出抛物线C1的解析式,并写出点G的坐标;
(2)如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】车间有20名工人,某一天他们生产的零件个数统计如下表:
生产零件的个数(个)
9
10
11
12
13
14
15
16
17
工人人数(人)
1
1
6
4
2
2
2
1
1
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以
 米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为
米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为 (米)与时间
(米)与时间 (分钟)的关系如图.请结合图象,解答下列问题:
(分钟)的关系如图.请结合图象,解答下列问题:
(1)填空:
 ______;
______;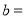 ______;
______; ______.
______.(2)求线段
 所在直线的解析式.
所在直线的解析式.(3)若小军的速度是120米/分,求小军第二次与爸爸相遇时距图书馆的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=﹣
 x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣
x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣ x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.
x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.(1)直接写出抛物线的解析式和点A,C,D的坐标;
(2)动点P在BD上以每秒2个单位长的速度由点B向点D运动,同时动点Q在CA上以每秒3个单位长的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒.PQ交线段AD于点E.
①当∠DPE=∠CAD时,求t的值;
②过点E作EM⊥BD,垂足为点M,过点P作PN⊥BD交线段AB或AD于点N,当PN=EM时,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:两个二次项系数之和为1,对称轴相同,且图象与y轴交点也相同的二次函数互为友好同轴二次函数
 例如:
例如: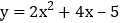 的友好同轴二次函数为
的友好同轴二次函数为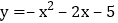 .
.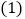 请你分别写出
请你分别写出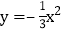 ,
,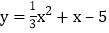 的友好同轴二次函数;
的友好同轴二次函数;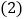 满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?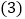 如图,二次函数
如图,二次函数 :
: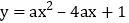 与其友好同轴二次函数
与其友好同轴二次函数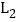 都与y轴交于点A,点B、C分别在
都与y轴交于点A,点B、C分别在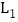 、
、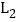 上,点B,C的横坐标均为
上,点B,C的横坐标均为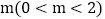 ,它们关于
,它们关于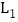 的对称轴的对称点分别为
的对称轴的对称点分别为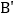 ,
,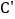 ,连结
,连结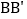 ,
,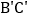 ,
,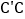 ,CB.
,CB. 若
若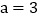 ,且四边形
,且四边形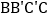 为正方形,求m的值;
为正方形,求m的值; 若
若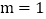 ,且四边形
,且四边形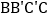 的邻边之比为1:2,直接写出a的值.
的邻边之比为1:2,直接写出a的值.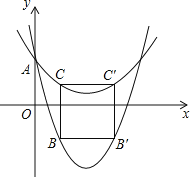
相关试题

