【题目】我们定义:两个二次项系数之和为1,对称轴相同,且图象与y轴交点也相同的二次函数互为友好同轴二次函数![]() 例如:
例如:![]() 的友好同轴二次函数为
的友好同轴二次函数为![]() .
.
![]() 请你分别写出
请你分别写出![]() ,
,![]() 的友好同轴二次函数;
的友好同轴二次函数;
![]() 满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
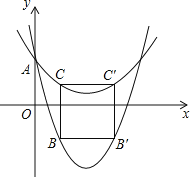
![]() 如图,二次函数
如图,二次函数![]() :
:![]() 与其友好同轴二次函数
与其友好同轴二次函数![]() 都与y轴交于点A,点B、C分别在
都与y轴交于点A,点B、C分别在![]() 、
、![]() 上,点B,C的横坐标均为
上,点B,C的横坐标均为![]() ,它们关于
,它们关于![]() 的对称轴的对称点分别为
的对称轴的对称点分别为![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,CB.
,CB.
![]() 若
若![]() ,且四边形
,且四边形![]() 为正方形,求m的值;
为正方形,求m的值;
![]() 若
若![]() ,且四边形
,且四边形![]() 的邻边之比为1:2,直接写出a的值.
的邻边之比为1:2,直接写出a的值.
参考答案:
【答案】![]() 函数
函数![]() 的友好同轴二次函数为
的友好同轴二次函数为![]() ;函数
;函数![]() 的友好同轴二次函数为
的友好同轴二次函数为![]() ;
;![]() 二次项系数为1的二次函数没有友好同轴二次函数;二次项系数为
二次项系数为1的二次函数没有友好同轴二次函数;二次项系数为![]() 的二次函数的友好同轴二次函数是它本身;
的二次函数的友好同轴二次函数是它本身;![]() 的值为
的值为![]() ;
;![]() 的值为
的值为![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)根据友好同轴二次函数的定义,找出![]() 、
、![]() 的友好同轴二次函数即可;
的友好同轴二次函数即可;
(2)由二次项系数非零可得出二次项系数为1的二次函数没有友好同轴二次函数,由友好同轴二次函数的定义可知:二次项系数为![]() 的二次函数的友好同轴二次函数是它本身;
的二次函数的友好同轴二次函数是它本身;
(3)根据二次函数L_1的解析式找出其友好同轴二次函数L_2的函数解析式.
①代入a=3,利用二次函数图象上点的坐标特征可得出点B、C、B'、C'的坐标,进而可得出BC、BB'的值,由正方形的性质可得出BC=BB',即关于m的一元二次方程,解之取其大于0小于2的值即可得出结论;
②由m=1,利用二次函数图象上点的坐标特征可得出点B、C、B'、C'的坐标,进而可得出BC、BB'的值,由两边之比为1:2,即可得出关于a的含绝对值符号的一元一次方程,解之即可得出结论.
![]() ,
,
![]() 函数
函数![]() 的友好同轴二次函数为
的友好同轴二次函数为![]() ;
;
![]() ,
,![]() ,
,
![]() 函数
函数![]() 的友好同轴二次函数为
的友好同轴二次函数为![]() .
.
![]() ,
,
![]() 二次项系数为1的二次函数没有友好同轴二次函数;
二次项系数为1的二次函数没有友好同轴二次函数;
![]() ,
,
![]() 二次项系数为
二次项系数为![]() 的二次函数的友好同轴二次函数是它本身.
的二次函数的友好同轴二次函数是它本身.
![]() 二次函数
二次函数![]() :
:![]() 的对称轴为直线
的对称轴为直线![]() ,其友好同轴二次函数
,其友好同轴二次函数![]() :
:![]() .
.
![]() ,
,
![]() 二次函数
二次函数![]() :
:![]() ,二次函数
,二次函数![]() :
:![]() ,
,
![]() 点B的坐标为
点B的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,![]() .
.
![]() 四边形
四边形![]() 为正方形,
为正方形,
![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() 不合题意,舍去
不合题意,舍去![]() ,
,
![]() 的值为
的值为![]() .
.
![]() 当
当![]() 时,点B的坐标为
时,点B的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,![]() .
.
![]() 四边形
四边形![]() 的邻边之比为1:2,
的邻边之比为1:2,
![]() 或
或![]() ,即
,即![]() 或
或![]() ,
,
解得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 的值为
的值为![]() 、
、![]() 、
、![]() 或
或![]() .
.
-
科目: 来源: 题型:
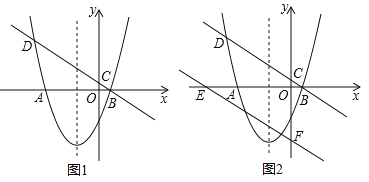
查看答案和解析>>【题目】如图1,抛物线y=ax2+2x+c与x轴交于A(﹣4,0),B(1,0)两点,过点B的直线y=kx+
 分别与y轴及抛物线交于点C,D.
分别与y轴及抛物线交于点C,D.(1)求直线和抛物线的表达式;
(2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;
(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以
 米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为
米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为 (米)与时间
(米)与时间 (分钟)的关系如图.请结合图象,解答下列问题:
(分钟)的关系如图.请结合图象,解答下列问题:
(1)填空:
 ______;
______;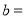 ______;
______; ______.
______.(2)求线段
 所在直线的解析式.
所在直线的解析式.(3)若小军的速度是120米/分,求小军第二次与爸爸相遇时距图书馆的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=﹣
 x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣
x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣ x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.
x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.(1)直接写出抛物线的解析式和点A,C,D的坐标;
(2)动点P在BD上以每秒2个单位长的速度由点B向点D运动,同时动点Q在CA上以每秒3个单位长的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒.PQ交线段AD于点E.
①当∠DPE=∠CAD时,求t的值;
②过点E作EM⊥BD,垂足为点M,过点P作PN⊥BD交线段AB或AD于点N,当PN=EM时,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数
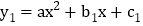 和
和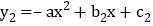 的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数
的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数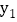 和
和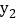 互为中心对称函数.
互为中心对称函数.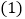 求函数
求函数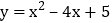 的中心对称函数;
的中心对称函数;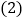 如图,在平面直角坐标系xOy中,E,F两点的坐标分别为
如图,在平面直角坐标系xOy中,E,F两点的坐标分别为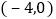 ,
,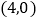 ,二次函数
,二次函数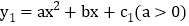 的图象经过点E和原点O,顶点为
的图象经过点E和原点O,顶点为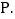 已知函数
已知函数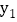 和
和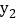 互为中心对称函数;
互为中心对称函数; 请在图中作出二次函数
请在图中作出二次函数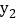 的顶点
的顶点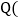 作图工具不限
作图工具不限 ,并画出函数
,并画出函数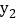 的大致图象;
的大致图象; 当四边形EPFQ是矩形时,请求出a的值;
当四边形EPFQ是矩形时,请求出a的值;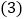 已知二次函数
已知二次函数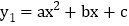 和
和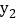 互为中心对称函数,且
互为中心对称函数,且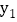 的图象经过
的图象经过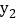 的顶点当
的顶点当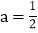 时,求代数式
时,求代数式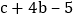 的最大值.
的最大值.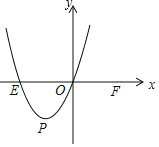
-
科目: 来源: 题型:
查看答案和解析>>【题目】亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,对于任意两点
 ,
, ,若点
,若点 满足
满足 ,
, 那么称点
那么称点 是点
是点 ,
, 的融合点,例如:
的融合点,例如: ,
, ,当点
,当点 满足
满足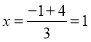 ,
, 时,则点
时,则点 是点
是点 ,
, 的融合点.
的融合点.(1)已知点
 ,
, ,
, ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.(2)如图,点
 ,点
,点 是直线
是直线 上任意一点,点
上任意一点,点 是点
是点 ,
, 的融合点.
的融合点.
①试确定
 与
与 的关系式;
的关系式;②在给定的坐标系
 中,画出①中的函数图象;
中,画出①中的函数图象;③若直线
 交
交 轴于点
轴于点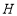 .当
.当 为直角三角形时,直接写出点
为直角三角形时,直接写出点 的坐标.
的坐标.
相关试题

