【题目】如图,已知△ABC.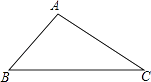
(1)利用直尺和圆规,按照下列要求作图(保留作图痕迹,不要求写作法)
①作∠ABC的平分线BD交AC于点D;
②作线段BD的垂直平分线分别交AB、BC于点E、F.
(2)连接DE,请判断线段DE与线段BF的数量关系,并说明理由.
参考答案:
【答案】
(1)解:如图所示

(2)解:DE=BF,
理由:∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵EF垂直平分BD,设垂足为O,
则OB=OD,BE=DE,
∴∠ABD=∠EDB,
∴∠DBC=∠EDB,
在△BOF和△DOE中,
 ,
,
∴△BOF≌△DOE(ASA),
∴DE=BF.
【解析】(1)根据全等三角形的判定方法SSS作出角平分线和垂直平分线;(2)根据角平分线和垂直平分线的性质,得到△BOF≌△DOE,根据全等三角形的对应边相等,得到DE=BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
某园林队计划由6名工人对180平方米的区域进行绿化,由于施工时增加了2名工人,结果比计划提前3小时完成任务,若每人每小时绿化面积相同,求每人每小时的绿化面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:(1)3x﹣12x3;(2)-2m+4m2-2m3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五边形的外角和是_______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽同学要画∠AOB的平分线,却没有量角器和圆规,于是她用三角尺按下面方法画角平分线:
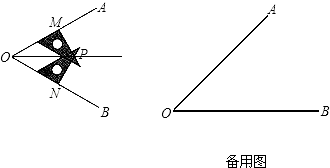
①在∠AOB的两边上,分别取OM=ON;
②分别过点M、N作OA、OB的垂线,交点为P;
③画射线OP,则OP为∠AOB的平分线.
(1)请问:小丽的画法正确吗?试证明你的结论;
(2)如果你现在只有刻度尺,能否画一个角的角平分线?请你在备用图中试一试.(不需要写作法,但是要让读者看懂,你可以在图中标明数据) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=﹣8,ab=12,则(a﹣b)2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)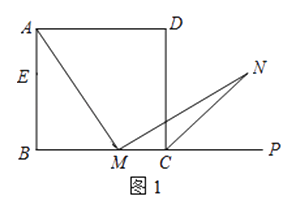
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.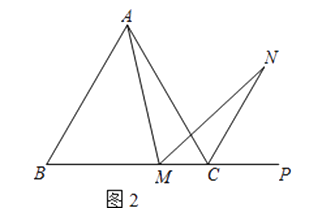
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN=时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
相关试题

