【题目】已知:如图数轴上两点A、B所别应的分别为﹣3、1,点P在数轴上从点A出发以每秒钟2个单位的长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.
(1)直接写出线段AB的中点所对应的数及t秒后点P所对应的数.
(2)若点P和点Q同时出发,求点P和点Q相遇时的位置所对应的数;
(3)若点P比点Q迟1秒钟出发,问点P出发几秒后,点P和点Q刚好相距1个单位长度.并问此时数轴上是否存在一个点C,使其到点A、点P和点Q这三点的距离和最小?若存在,直接写出点C所对应的数;若不存在,试说明理由.
![]()
参考答案:
【答案】(1)点P所对应的数是﹣3+2t;(2)-![]() ;(3)存在,当P出发
;(3)存在,当P出发![]() 秒或
秒或![]() 秒时,P和Q相距1个单位长度,此时点C所表示的数分别为﹣
秒时,P和Q相距1个单位长度,此时点C所表示的数分别为﹣![]() 和﹣
和﹣![]()
【解析】
(1)根据点A表示的数为-3,点B表示的数为1,根据中点坐标公式即可得到AB的中点所对应的数,进一步利用点的平移规律求得点P对应的数;
(2)可设经过x秒钟点P和点Q相遇,由路程和是AB的长,列出方程求解,进一步得出相遇点的位置即可;
(3)设点P出发y秒后,点P和点Q刚好相距1个单位长度,列出方程解答,分别求得P、Q点表示的数,设出点C表示的数,进一步利用两点之间的距离求得最小值即可.
(1)线段AB的中点所对应的数是![]() =﹣1,点P所对应的数是﹣3+2t;
=﹣1,点P所对应的数是﹣3+2t;
(2)设经过x秒钟点P和点Q相遇,由题意得
2x+x=1﹣(﹣3)
解得:x=![]() ,
,
点P和点Q相遇时的位置所对应的数为﹣3+2×![]() =﹣
=﹣![]() ;
;
(3)①设点P出发y秒后,点P和点Q刚好相距1个单位长度,由题意得
y12y+y=4﹣1,
解得:y=![]() ,
,
点P表示为﹣3+![]() ×2=﹣
×2=﹣![]() ,点Q表示为1﹣(1+
,点Q表示为1﹣(1+![]() )×1=﹣
)×1=﹣![]() ,
,
设此时数轴上存在一个点C,点C表示的数为a,由题意得
AC+PC+QC=|a+3|+|a+![]() |+|a+
|+|a+![]() |,
|,
要使|a+3|+|a+![]() |+|a+
|+|a+![]() |最小,当点C与P重合时,即a=﹣
|最小,当点C与P重合时,即a=﹣![]() 时,点C,使其到点A、点P和点Q这三点的距离和最小.
时,点C,使其到点A、点P和点Q这三点的距离和最小.
②若点P和点Q在相遇后相距1个单位长度,则2t=1×(t+1)=4+1
解得t=![]()
故P出发![]() 秒后,点P和点Q也可相距1个单位长度
秒后,点P和点Q也可相距1个单位长度
此时满足条件的点C即点Q,所表示的数位﹣![]()
综上所述,当P出发![]() 秒或
秒或![]() 秒时,P和Q相距1个单位长度,此时点C所表示的数分别为﹣
秒时,P和Q相距1个单位长度,此时点C所表示的数分别为﹣![]() 和﹣
和﹣![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距400km,甲、乙两车分别从A、B两地同时出发,相向而行,甲车以每小时100km的速度匀速行驶1h后,休息了1h,然后按原速继续行驶到B地,乙车以每小时80km的速度匀速行驶到A地.
(1)当乙车经过甲车休息的地方时,乙车行驶的时间是 h;
(2)当甲、乙两车相遇时,求乙车行驶的时间;
(3)当甲、乙两车相距40km时,求乙车行驶的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近一个月来,某地区连受暴雨袭击,江水水位上涨,小明以警戒水位为0点,用折线统计图表示某一天江水水位情况。请你结合如图所示的折线统计图判断下列叙述,其中错误的是( )

A. 8时水位最高 B. 这一天水位均高于警戒水位
C. 8时到16时水位都在下降 D. 点P表示12时沙拉高于警戒水位0.6米
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂第一车间有x人,第二车间比第一车间人数的
 少20人,如果从第二车间调出15人到第一车间,那么
少20人,如果从第二车间调出15人到第一车间,那么(1)调动后,第一车间的人数为 人;第二车间的人数为 人.
(2)调动后,第一车间的人数比第二车间的人数多多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( )
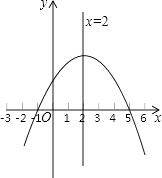
A.ac<0
B.a﹣b+c>0
C.b=﹣4a
D.关于x的方程ax2+bx+c=0的根是x1=﹣1,x2=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】P是正方形ABCD的BC边上一点,连结AP,AB=8,BP=3,Q是线段AP上一动点,连结BQ并延长交四边形ABCD的一边于点R,若点Q是BR的三等分点,则AR的长为
相关试题

