【题目】P是正方形ABCD的BC边上一点,连结AP,AB=8,BP=3,Q是线段AP上一动点,连结BQ并延长交四边形ABCD的一边于点R,若点Q是BR的三等分点,则AR的长为
参考答案:
【答案】![]() 或6或
或6或 ![]()
【解析】解:如图1中,①当BQ1=2Q1R1时,
∵AD∥BC,
∴ ![]() =
= ![]() =
= ![]() ,∵PB=3,
,∵PB=3,
∴AR1= ![]() ,
,
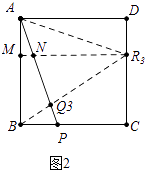
②当Q2R2=2BQ2时,
∵AR2∥PB,
∴ ![]() =
= ![]() =2,
=2,
∴AR2=6.
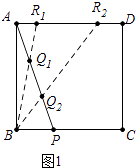
③如图2中,当点R3在CD上时,R3Q3=2BQ3 , 作R3M⊥AB于M,交AP于N.
∵R3N∥PB,
∴ ![]() =
= ![]() =2,
=2,
∴NR3=6,MN=MR3=AD=8﹣6=2,
∵MN∥PB,
∴ ![]() =
= ![]() ,
,
∴AM= ![]() ,
,
在RT△AMR3中,AR3= ![]() =
= ![]() =
= ![]() .
.
所以答案是 ![]() 或6或
或6或 ![]() .
.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图数轴上两点A、B所别应的分别为﹣3、1,点P在数轴上从点A出发以每秒钟2个单位的长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.
(1)直接写出线段AB的中点所对应的数及t秒后点P所对应的数.
(2)若点P和点Q同时出发,求点P和点Q相遇时的位置所对应的数;
(3)若点P比点Q迟1秒钟出发,问点P出发几秒后,点P和点Q刚好相距1个单位长度.并问此时数轴上是否存在一个点C,使其到点A、点P和点Q这三点的距离和最小?若存在,直接写出点C所对应的数;若不存在,试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂第一车间有x人,第二车间比第一车间人数的
 少20人,如果从第二车间调出15人到第一车间,那么
少20人,如果从第二车间调出15人到第一车间,那么(1)调动后,第一车间的人数为 人;第二车间的人数为 人.
(2)调动后,第一车间的人数比第二车间的人数多多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( )
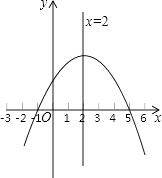
A.ac<0
B.a﹣b+c>0
C.b=﹣4a
D.关于x的方程ax2+bx+c=0的根是x1=﹣1,x2=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】八年级(1)班有48名学生,春游前,班长把全班学生对春游地点的意向绘制成了扇形统计图,其中“想去动物园的学生数”的扇形圆心角为60°,则下列说法正确的是( )
A. 想去动物园的学生占全班学生的60% B. 想去动物园的学生有12人
C. 想去动物园的学生肯定最多 D. 想去动物园的学生占全班学生的

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司要把
 吨白砂糖运往
吨白砂糖运往 、
、 两地,用大、小两种货车共
两地,用大、小两种货车共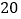 辆,恰好一次可以运完.已知大、小货车的载重量分别为
辆,恰好一次可以运完.已知大、小货车的载重量分别为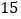 吨/辆和
吨/辆和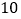 吨/辆,运往
吨/辆,运往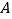 地的运费为大货车
地的运费为大货车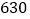 元/辆,小货车
元/辆,小货车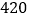 元/辆,运往
元/辆,运往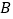 地的运费为大货车
地的运费为大货车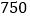 元/辆,小货车
元/辆,小货车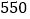 元/辆.
元/辆.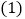 求两种货车各用多少辆;
求两种货车各用多少辆;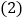 如果安排
如果安排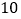 辆货车前往
辆货车前往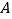 地,剩下的货车前往
地,剩下的货车前往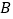 地,那么当前往
地,那么当前往 地的大货车有多少辆时,总运费为
地的大货车有多少辆时,总运费为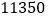 元.
元. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,AB∥EG∥x轴,BC∥DE∥HG∥AP∥y轴,点D、C、P、H在x轴上,A(1,2),B(﹣1,2),D(﹣3,0),E(﹣3,﹣2),G(3,﹣2),把一条长为2018个单位长度且没有弹性的细线线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣E﹣F﹣G﹣H﹣﹣P﹣A…的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是( )

A. (1,2)B. (﹣1,2)C. (﹣1,0)D. (1,0)
相关试题

