【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
参考答案:
【答案】(1)33°(2)证明见解析
【解析】(1)解:∵AB∥CD,∴∠ACD+∠CAB=180°。
又∵∠ACD=114°,∴∠CAB=66°。
由作法知,AM是∠ACB的平分线,∴∠AMB=![]() ∠CAB=33°。
∠CAB=33°。
(2)证明:∵AM平分∠CAB,∴∠CAM=∠MAB,
∵AB∥CD,∴∠MAB=∠CMA。∴∠CAN=∠CMN。
又∵CN⊥AM,∴∠ANC=∠MNC。
在△ACN和△MCN中,
∵∠ANC=∠MNC,∠CAN=∠CMN,CN=CN,∴△ACN≌△MCN(AAS)。
(1)由作法知,AM是∠ACB的平分线,由AB∥CD,根据两直线平行同旁内角互补的性质,得∠CAB=66°,从而求得∠MAB的度数。
(2)要证△ACN≌△MCN,由已知,CN⊥AM即∠ANC=∠MNC=90°;又CN是公共边,故只要再有一边或一角相等即可,考虑到AB∥CD和AM是∠ACB的平分线,有∠CAN=∠MAB =∠CMN。
从而得证。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产的商品市场指导价为每千克150元,公司的实际销售价格可以浮动x个百分点(即销售价格=150(1+x%)),经过市场调研发现,这种商品的日销售量p(千克)与销售价格浮动的百分点x之间的函数关系为p=﹣2x+24.若该公司按浮动﹣12个百分点的价格出售,每件商品仍可获利10%.
(1)求该公司生产销售每千克商品的成本为多少元?
(2)当该公司的商品定价为多少元时,日销售利润为576元?(说明:日销售利润=(销售价格一成本)×日销售量)
(3)该公司决定每销售一千克商品就捐赠a元利润(a≥1)给希望工程,公司通过销售记录发现,当价格浮动的百分点大于﹣1时,扣除捐赠后的日销售利润随x的增大而减小,直接写出a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C1:y=x2+2x﹣3与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线C2:y=ax2+bx+c经过点B,与x轴的另一个交点为E(﹣4,0),与y轴交于点D(0,2).
(1)求抛物线C2的解析式;
(2)设点P为线段AB上一动点(点P不与点A,B重合),过点P作x轴的垂线交抛物线C1于点M,交抛物线C2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.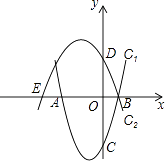
-
科目: 来源: 题型:
查看答案和解析>>【题目】松雷中学刚完成一批校舍的修建,有一些相同的办公室需要粉刷墙面.一天3名一级技工去粉刷7个办公室,结果其中有90m2墙面未来得及粉刷;同样时间内4名二级技工粉刷了7个办公室之外,还多粉刷了另外的70m2墙面.每名一级技工比二级技工一天多粉刷40m2墙面.
(1)求每个办公室需要粉刷的墙面面积.
(2)已知每名一级技工每天需要支付费用100元,每名二级技工每天需要支付费用90元.松雷中学有40个办公室的墙面和720m2的展览墙需要粉刷,现有3名一级技工的甲工程队,4名二级技工的乙工程队,要来粉刷墙面.松雷中学有两个选择方案,方案一:全部由甲工程队粉刷;方案二:全部由乙工程队粉刷;若使得总费用最少,松雷中学应如何选择方案,请通过计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距400km,甲、乙两车分别从A、B两地同时出发,相向而行,甲车以每小时100km的速度匀速行驶1h后,休息了1h,然后按原速继续行驶到B地,乙车以每小时80km的速度匀速行驶到A地.
(1)当乙车经过甲车休息的地方时,乙车行驶的时间是 h;
(2)当甲、乙两车相遇时,求乙车行驶的时间;
(3)当甲、乙两车相距40km时,求乙车行驶的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近一个月来,某地区连受暴雨袭击,江水水位上涨,小明以警戒水位为0点,用折线统计图表示某一天江水水位情况。请你结合如图所示的折线统计图判断下列叙述,其中错误的是( )

A. 8时水位最高 B. 这一天水位均高于警戒水位
C. 8时到16时水位都在下降 D. 点P表示12时沙拉高于警戒水位0.6米
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图数轴上两点A、B所别应的分别为﹣3、1,点P在数轴上从点A出发以每秒钟2个单位的长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.
(1)直接写出线段AB的中点所对应的数及t秒后点P所对应的数.
(2)若点P和点Q同时出发,求点P和点Q相遇时的位置所对应的数;
(3)若点P比点Q迟1秒钟出发,问点P出发几秒后,点P和点Q刚好相距1个单位长度.并问此时数轴上是否存在一个点C,使其到点A、点P和点Q这三点的距离和最小?若存在,直接写出点C所对应的数;若不存在,试说明理由.

相关试题

