【题目】(2016山西省)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg﹣5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

参考答案:
【答案】(1)方案A:函数表达式为y=5.8x;方案B:函数表达式为y=5x+2000;(2)2000≤x<2500;(3)方案B买的苹果多.
【解析】试题分析:(1)根据数量关系列出函数表达式即可;(2)先求出方案A应付款y与购买量x的函数关系为![]() ,方案B 应付款y与购买量x的函数关系为
,方案B 应付款y与购买量x的函数关系为![]() ,然后分段求出哪种方案付款少即可;(3)令y=20000,分别代入A方案和B方案的函数关系式中,求出x,比大小.
,然后分段求出哪种方案付款少即可;(3)令y=20000,分别代入A方案和B方案的函数关系式中,求出x,比大小.
试题解析:(1)方案A:函数表达式为![]() .
.
方案B:函数表达式为![]()
(2)由题意,得![]() .
.
解不等式,得x<2500
∴当购买量x的取值范围为![]() 时,选用方案A比方案B付款少.
时,选用方案A比方案B付款少.
(3)他应选择方案B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一根长为1米的木杆,第1次截取其长度的一半,第2次截取其第1次剩下长度的一半,第3次截取其第2次剩下长度的一半,如此反复截取,则第n(n为正整数)次截取后,此木杆剩下的长度为米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技的发展,电动汽车的性能得到显著提高,某市对市场上电动汽车的性能进行随机抽样调查,现随机抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据绘制成如下频数分布直方表和条形统计图.
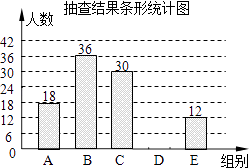
根据以上信息回答下列问题:组别
行驶里程x(千米)
频数(台)
频率
A
x<200
18
0.15
B
200≤x<210
36
a
C
210≤x<220
30
0.25
D
220≤x<230
b
0.20
E
x≥230
12
0.10
根据以上信息回答下列问题:
(1)填空:a= , b=;
(2)请将条形统计图补充完整;
(3)若该市市场上的电动汽车有2000台,请你估计电动汽车一次充电后行驶的里程数在220千米及以上的台数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B,C,D四个点不在同一直线上,根据下列语句画图.
(1)画射线AB,画直线AC,画线段AD;
(2)连接BD与直线AC相交于点E;
(3)延长线段BC,反向延长线段DC;
(4)若在上述所画的图形中,设从点D到点C有四条路径,它们分别是①D→A→B→C;②D→B→C;③D→E→C;④D→C;哪条道路最短?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】星期天的早晨,小明骑自行车从家出发,到离家1050米的书店买书,出发1分钟后,他到达离家150米的地方,又过1分钟后,小明加快了速度.如图所示是小明从家出发后离家的路程y(米)与他骑自行车的时间x(分钟)之间的函数图象.根据图象解答下列问题:
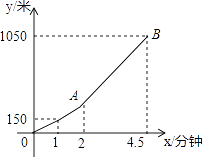
(1)直接写出点A的坐标,并求线段AB所在的直线的函数解析式.
(2)求小明出发多长时间后,离书店还剩210米的路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在棋盘中建立如图的直角坐标系,三颗棋子A,O,B的位置如图,它们分别是(-1,1),(0,0)和(1,0).
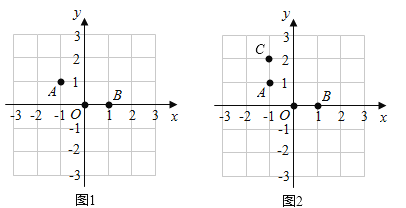
(1)如图2,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴;
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地。假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等,)又顺水航行返回万州,若该轮船从万州出发后所用时间为x(小时),轮船距万州的距离为y(千米),则下列各图中,能反映y与x之间函数关系的图象大致是【 】
A.
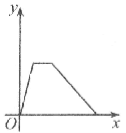 B.
B.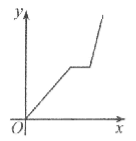 C.
C.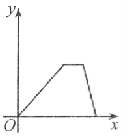 D.
D.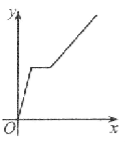
相关试题

