【题目】如图,需在一面墙上绘制两个形状相同的抛物绒型图案,按照图中的直角坐标系,最高点M到横轴的距离是4米,到纵轴的距离是6米;纵轴上的点A到横轴的距离是1米,右侧抛物线的最大高度是左侧抛物线最大高度的一半.(结果保留整数或分数,参考数据: ![]() =
= ![]() ,
, ![]() =
= ![]() )
) 
(1)求左侧抛物线的表达式;
(2)求右侧抛物线的表达式;
(3)求这个图案在水平方向上的最大跨度是多少米.
参考答案:
【答案】
(1)解:最高点M到横轴的距离是4米,到纵轴的距离是6米
∴M(6,4),
设左侧抛物线的表达式为y=a(x﹣6)2+4,
把A(0,1)代入y=a(x﹣6)2+4得a=﹣ ![]() ,
,
∴左侧抛物线的表达式为y=﹣ ![]() (x﹣6)2+4
(x﹣6)2+4
(2)解:∵抛物线y=﹣ ![]() (x﹣6)2+4与x轴的交点C(13,0),
(x﹣6)2+4与x轴的交点C(13,0),
∵右侧抛物线与左侧抛物线形状相同,
∴设右侧抛物线的表达式为y=﹣ ![]() (x﹣h)2+2,
(x﹣h)2+2,
把C(13,0)代入y=﹣ ![]() (x﹣h)2+2得0=﹣
(x﹣h)2+2得0=﹣ ![]() (13﹣h)2+2,
(13﹣h)2+2,
解得:h=18,h=8(不合题意,舍去),
∴右侧抛物线的表达式为y=﹣ ![]() (x﹣18)2+2
(x﹣18)2+2
(3)解:∵C(13,0),右侧抛物线的对称轴是直线x=18,
∴D(23,0),
∴这个图案在水平方向上的最大跨度是23米
【解析】(1)根据已知条件得到M(6,4),设左侧抛物线的表达式为y=a(x﹣6)2+4,把A(0,1)代入y=a(x﹣6)2+4即可得到结论;(2)根据(1)中的结论设右侧抛物线的表达式为y=﹣ ![]() (x﹣h)2+2,把C(13,0)代入y=﹣
(x﹣h)2+2,把C(13,0)代入y=﹣ ![]() (x﹣h)2+2即可得到结论;(3)求出D(23,0),于是得到结论.
(x﹣h)2+2即可得到结论;(3)求出D(23,0),于是得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,P是第一象限角平分线上的一点,且P点的横坐标为3.把一块三角板的直角顶点固定在点P处,将此三角板绕点P旋转,在旋转的过程中设一直角边与x轴交于点E,另一直角边与y轴交于点F,若△POE为等腰三角形,则点F的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回.如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)直接写出y甲,y乙与x之间的函数关系式(不写过程);
(2)①求出点M的坐标,并解释该点坐标所表示的实际意义;
②根据图象判断,x取何值时,y乙>y甲.

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题
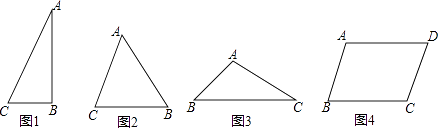
【问题提出】
已知任意三角形的两边及夹角(是锐角),求三角形的面积.
【问题探究】
为了解决上述问题,让我们从特殊到一般展开探究.
探究:在Rt△ABC(图1)中,∠ABC=90°,AC=b,BC=a,∠C=α,求△ABC的面积(用含a、b、α的代数式表示)
在Rt△ABC中,∠ABC=90°
∴sinα=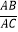
∴AB=bsinα
∴S△ABC= BCAB=
BCAB=  absinα
absinα
(1)探究一:
锐角△ABC(图2)中,AC=b,BC=a,∠C=α(0°<α<90°)
求:△ABC的面积.(用含a、b、α的代数式表示)
(2)探究二:
钝角△ABC(图3)中,AC=b,BC=a,∠C=α(0°<α<90°)
求:△ABC的面积.(用含a、b、α的代数式表示)
(3)【问题解决】
用文字叙述:已知任意三角形的两边及夹角(是锐角),求三角形面积的方法
是
(4)已知平行四边形ABCD(图4)中,AB=b,BC=a,∠B=α(0°<α<90°)
求:平行四边形ABCD的面积.(用含a、b、α的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)

相关试题

