【题目】如图,圆E是三角形ABC的外接圆, ∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分别以BC、AO所在直线建立x轴.
(1)求三角形ABC的外接圆直径;
(2)求过ABC三点的抛物线的解析式;
(3)设P是(2)中抛物线上的一个动点,且三角形AOP为直角三角形,则这样的点P有几个?(只需写出个数,无需解答过程).

参考答案:
【答案】(1)![]() ;(2)抛物线的解析式为y=-x2+x+6.(3)满足条件的点P有6个.
;(2)抛物线的解析式为y=-x2+x+6.(3)满足条件的点P有6个.
【解析】试题分析:(1)如图1中,连接EB、EC.由BC=OB+OC=5,∠BEC=2∠BC=90°,可知EB的长,进而得到结论.
(2)如图2中,作EM⊥BC于M,EN⊥OA于N,连接AE,则四边形EMON是矩形.利用勾股定理求出点A、B、C三点坐标,利用待定系数法即可解决问题.
(3)①以OA为直径画圆与抛物线有4个交点,根据直径所对的圆周角是直角,可知这样有4个点P满足条件.②当PA⊥OA时,有一个点P满足条件.③当PO⊥OA时,有两个点P满足条件.
试题解析:解:(1)如图1中,连接EB、EC.
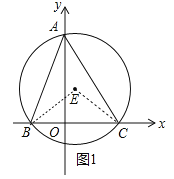
∵BC=OB+OC=5,∠BEC=2∠BC=90°,∴EB=EC=![]() ,∴⊙E的直径为
,∴⊙E的直径为![]() .
.
(2)如图2中,作EM⊥BC于M,EN⊥OA于N,连接AE,则四边形EMON是矩形.
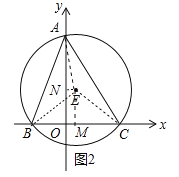
在Rt△EMC中,EM=ON=![]() =
= =
=![]() ,OM=NE=OC﹣CM=
,OM=NE=OC﹣CM=![]() ,在Rt△EN中,AN=
,在Rt△EN中,AN=![]() =
= =
=![]() ,∴OA=AN+ON=6,∴A(0,6),B(﹣2,0),C(3,0),设抛物线的解析式为y=a(x+2)(x﹣3),把(0,6)的坐标代入得a=﹣1,∴抛物线的解析式为y=﹣x2+x+6.
,∴OA=AN+ON=6,∴A(0,6),B(﹣2,0),C(3,0),设抛物线的解析式为y=a(x+2)(x﹣3),把(0,6)的坐标代入得a=﹣1,∴抛物线的解析式为y=﹣x2+x+6.
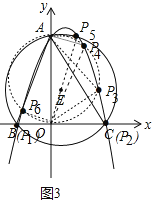
(3)如图3中,①以OA为直径画圆与抛物线有4个交点,根据直径所对的圆周角是直角,可知这样有4个点P满足条件.
②当PA⊥OA时,有一个点P满足条件.
③当PO⊥OA时,有两个点P满足条件.
所以满足条件的点P有6个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、室O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2018秒时,点P的坐标是( )
个单位长度,则第2018秒时,点P的坐标是( )
A. (2017,0)B. (2018,﹣1)C. (2017,1)D. (2018,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空并完成推理过程.
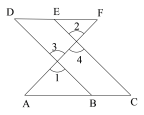
如图,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
证明:∵∠1=∠2(已知)
∠1=∠3(对顶角相等)
∴∠2=∠3( )
∴____∥______( )
∴∠C=∠ABD( )
又∵∠C=∠D(已知)
∴∠D=∠ABD(等量代换)
∴AC∥DF( )
-
科目: 来源: 题型:
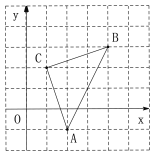
查看答案和解析>>【题目】如图,直角坐标系中,三角形ABC的顶点都在网格点上,其中A(2,
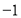 ), B(4,3), C(1,2).
), B(4,3), C(1,2).(1)将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形
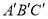 ,则三角形
,则三角形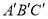 的三个顶点坐标。
的三个顶点坐标。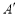 ( ),
( ),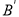 ( ),
( ),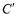 ( ).
( ).(2)求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 (1)①如图1,已知AB∥CD,∠ABC=60°,可得∠BCD=_______°;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM=_________°;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN=___________°.
(2)、尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线, CN⊥CM,求∠BCM的度数.
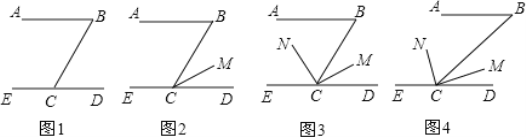
-
科目: 来源: 题型:
查看答案和解析>>【题目】书店老板去图书批发市场购买某种图书,第一次用1200元购买若干本,很快售完.第二次购买时,每本书的进价比第一次提高了20%,他用1500元所购买的数量比第一次多10本.求第一次购买的图书,每本进价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为矩形,点E是边BC的中点,AF∥ED,AE∥DF
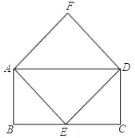
(1)求证:四边形AEDF为菱形;
(2)试探究:当AB:BC= ,菱形AEDF为正方形?请说明理由.
相关试题

