【题目】有一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从
某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)
与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:

①每分钟进水5升;②当4≤x≤12时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以上说法中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】
根据图象可以得到单独打开进水管4分钟注水20升,而同时打开放水管,8分钟内放进10升水,据此即可解答.
解:①每分钟进水![]() =5升,则命题正确;
=5升,则命题正确;
②当4≤x≤12时,y随x的增大而增大,因而容器中水量在增加,则命题错误;
③每分钟放水5-![]() =5-1.25=3.75升,
=5-1.25=3.75升,
则放完水需要![]() =8(分钟),故命题正确;
=8(分钟),故命题正确;
④同时打开进水管和放水管,每分钟进水![]() =1.25升,则同时打开需要将容器灌满需要的时间是
=1.25升,则同时打开需要将容器灌满需要的时间是![]() =24(分钟),命题正确.
=24(分钟),命题正确.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用两种正多边形铺满地面,其中一种是正八边形,则另一种正多边形是( )。
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:AE=CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,后解答:
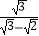 =
= 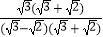 =
= 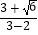 =3+
=3+ 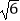
像上述解题过程中,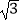 ﹣
﹣ 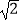 与
与 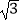 +
+ 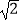 相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)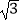 的有理化因式是;
的有理化因式是; 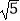 +2的有理化因式是
+2的有理化因式是
(2)将下列式子进行分母有理化: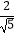 =;
=; 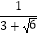 = .
= .
(3)已知a=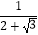 ,b=2﹣
,b=2﹣ 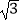 ,比较a与b的大小关系.
,比较a与b的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
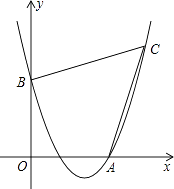
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
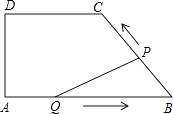
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
相关试题

