【题目】如图,已知四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:AE=CF. 
参考答案:
【答案】证明:∵四边形ABCD是平行四边形, ∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∴180°﹣∠ABD=180°﹣∠CDB,
即∠ABE=∠CDF,
在△ABE和△CDF中,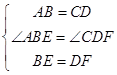 ,
,
∴△ABE≌△CDF(SAS),
∴AE=CF
【解析】根据平行四边形的对边相等可得AB=CD,AB∥CD,再根据两直线平行,内错角相等可得∠ABD=∠CDB,然后求出∠ABE=∠CDF,再利用“边角边”证明△ABE和△CDF全等,根据全等三角形对应边相等证明即可.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR,②QP∥AR,③△BPR≌△QPS中一定正确的是( )

A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】用两种正多边形铺满地面,其中一种是正八边形,则另一种正多边形是( )。
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从
某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)
与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:

①每分钟进水5升;②当4≤x≤12时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以上说法中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,后解答:
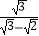 =
= 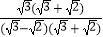 =
= 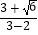 =3+
=3+ 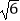
像上述解题过程中,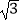 ﹣
﹣ 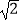 与
与 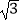 +
+ 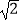 相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)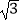 的有理化因式是;
的有理化因式是; 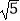 +2的有理化因式是
+2的有理化因式是
(2)将下列式子进行分母有理化: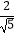 =;
=; 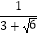 = .
= .
(3)已知a=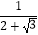 ,b=2﹣
,b=2﹣ 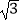 ,比较a与b的大小关系.
,比较a与b的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
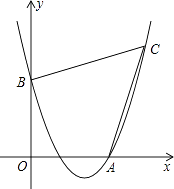
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
相关试题

