【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题: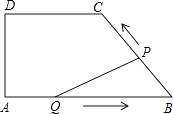
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
参考答案:
【答案】
(1)
解:作CE⊥AB于E,
∵DC∥AB,DA⊥AB,
∴四边形AECD是矩形,
∴AE=CD=5,CE=AD=4,
∴BE=3,
∴BC= ![]() ,
,
∴BC<AB,
∴P到C时,P、Q同时停止运动,
∴t= ![]() (秒),
(秒),
即t=5秒时,P,Q两点同时停止运动
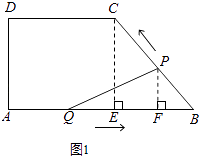
(2)
解:由题意知,AQ=BP=t,
∴QB=8﹣t,
作PF⊥QB于F,则△BPF~△BCE,
∴ ![]() ,即
,即 ![]() ,
,
∴BF= ![]() ,
,
∴S= ![]() QBPF=
QBPF= ![]() ×
× ![]() (8﹣t)=
(8﹣t)= ![]() =﹣
=﹣ ![]() (t﹣4)2+
(t﹣4)2+ ![]() (0<t≤5),
(0<t≤5),
∵﹣ ![]() <0,
<0,
∴S有最大值,当t=4时,S的最大值是 ![]()
(3)
解:∵cos∠B= ![]() ,
,
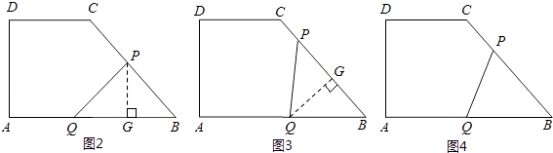
① 当PQ=PB时(如图2所示),则BG= ![]() BQ,
BQ, ![]() =
= ![]() =
= ![]() ,解得t=
,解得t= ![]() s,
s,
②当PQ=BQ时(如图3所示),则BG= ![]() PB,
PB, ![]() =
= ![]() =
= ![]() ,解得t=
,解得t= ![]() s,
s,
③当BP=BQ时(如图4所示),则8﹣t=t,
解得:t=4.
综上所述:当t= ![]() s,
s, ![]() s或t=4s时,△PQB为等腰三角形
s或t=4s时,△PQB为等腰三角形
【解析】(1)通过比较线段AB,BC的大小,找出较短的线段,根据速度公式可以直接求得;(2)由已知条件,把△PQB的边QB用含t的代数式表示出来,三角形的高可由相似三角形的性质也用含t的代数式表示出来,代入三角形的面积公式可得到一个二次函数,即可求出S的最值;(3)根据等腰三角形的性质和余弦公式列出等式求解,即可求的结论.
【考点精析】利用相似三角形的应用对题目进行判断即可得到答案,需要熟知测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从
某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)
与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:

①每分钟进水5升;②当4≤x≤12时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以上说法中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,后解答:
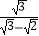 =
= 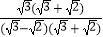 =
= 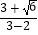 =3+
=3+ 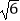
像上述解题过程中,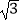 ﹣
﹣ 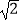 与
与 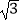 +
+ 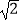 相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)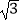 的有理化因式是;
的有理化因式是; 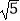 +2的有理化因式是
+2的有理化因式是
(2)将下列式子进行分母有理化: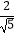 =;
=; 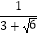 = .
= .
(3)已知a=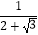 ,b=2﹣
,b=2﹣ 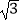 ,比较a与b的大小关系.
,比较a与b的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
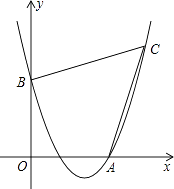
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴的交点坐标为(-2,0),则下列说法:①y随x的增大而减小;②关于x的方程kx+b=0的解为x=-2;③kx+b>0的解集是x>-2;④b<0.其中正确的有__________.(填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=kx﹣2中,y随x的增大而减小,则它的图像可以是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值范围是( )

A.h≤17cm
B.h≥8cm
C.15cm≤h≤16cm
D.7cm≤h≤16cm
相关试题

