【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
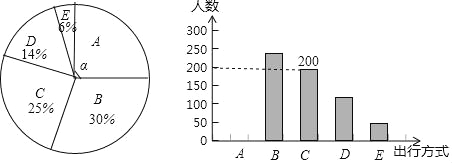
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
参考答案:
【答案】(1)800人,240人(2)200人(3)9.6万人
【解析】
试题分析:(1)由C类别人数及其百分比可得总人数,总人数乘以B类别百分比即可得;
(2)根据百分比之和为1求得A类别百分比,再乘以360°和总人数可分别求得;
(3)总人数乘以样本中A、B、C三类别百分比之和可得答案.
试题解析:(1)本次调查的市民有200÷25%=800(人),
∴B类别的人数为800×30%=240(人),
故答案为:800,240;
(2)∵A类人数所占百分比为1﹣(30%+25%+14%+6%)=25%,
∴A类对应扇形圆心角α的度数为360°×25%=90°,A类的人数为800×25%=200(人),
补全条形图如下:
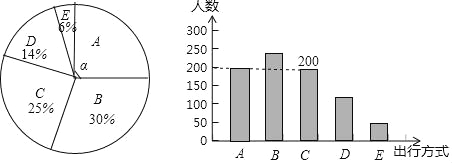
(3)12×(25%+30%+25%)=9.6(万人),
答:估计该市“绿色出行”方式的人数约为9.6万人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a,b,c为常数,a≠0),其中自变量x与函数值y之间满足下面的对应关系:
x
…
3
5
7
…
y
…
2.5
2.5
﹣1.5
…
则a+b+c=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的周长为30cm,一边长为16cm,则腰长为( )
A. 16cm B. 7cm C. 16cm或7cm D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.
B.3a﹣2=
C.(﹣1)0=1
D.00=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解并在括号内填注理由:
如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
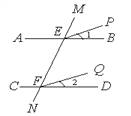
证明:∵AB∥CD,
∴∠MEB=∠MFD(_____________)
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥____.(_______________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(2x﹣4,x2+2)在y轴上,则点M的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
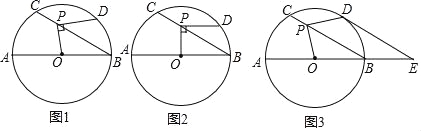
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当
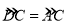 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=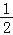 AB,连接DE.
AB,连接DE.①求证:DE是⊙O的切线;
②求PC的长.
相关试题

