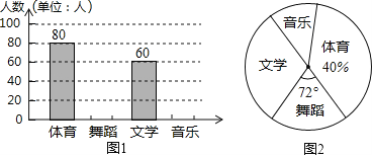
【题目】为了促进学生多样化发展,某中学每周五组织学生开展社团活动,分别设置了体育、舞蹈、文学、音乐社团(要求人人参加社团,并且每人只能参加一项),为了解学生喜欢哪种社团活动,学校组织学生会成员随机抽取部分学生进行问卷调查,根据收集到的数据,绘制成了两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(1)此次共调查了______名学生;
(2)将条形统计图补充完整;
(3)图2中音乐社团所在扇形的圆心角的度数为______;
(4)若该校共有学生1600人,估计该校喜爱体育社团的学生人数.
参考答案:
【答案】(1)200;(2)补图见解析;(3)36°;(4)640人.
【解析】
(1)从条形统计图中可以获得体育的人数为80人,从扇形统计图中可以得到体育的人数占调查人数的40%,可求出调查的人数;
(2)求出舞蹈人数、音乐人数,即可补全条形统计图;
(3)求出参与音乐社团人数所占的百分比乘以360°计算即可;;
(4)样本估计总体,喜欢体育的人数占整体人数1600人的40%即可.
解:(1)80÷40%=200人
故答案为:200.
(2)舞蹈的人数:200×![]() =40人
=40人
音乐的人数为:200-80-60-40=20人,补全条形统计图如图所示:

(3)360°×![]() =36°
=36°
答:音乐的圆心角度数为:36°.
(4)1600×40%=640人,
答:该校1600人学生中喜爱体育社团的学生人数为640人
-
科目: 来源: 题型:
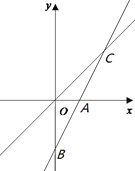
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+ b的图象分别与x轴和y轴交于点A、B(0,-2),与正比例函数y=x的图象交于点C(m,2).
(1)求m的值和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出使函数y =kx +b的值大于函数y=x的值的自变量x的取值范围.
-
科目: 来源: 题型:
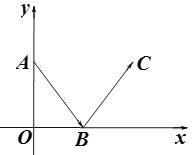
查看答案和解析>>【题目】如图,从点A(0,4)出发的一束光,经x轴反射,过点C(6,4),求这束光从点A到点C所经过的路径长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.
(1)请你添加一个适当的条件 ,使得四边形ABCD是平行四边形,并证明你的结论;
(2)作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(3)在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF=
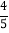 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AB∥CD,直线EF分别交AB、CD于A、C,CM是∠ACD的平分线,CM交AB于H,过A作AG⊥AC交CM于G.
(1)如图1,点G在CH的延长线上时,
①若∠GAB=36°,则∠MCD=______.
②猜想:∠GAB与∠MCD之间的数量关系是______.
(2)如图2,点G在CH上时,(1)②猜想的∠GAB与∠MCD之间的数量关系还成立吗?如果成立,请给出证明;如果不成立,请写出∠GAB与∠MCD之间的数量关系,并说明理由.
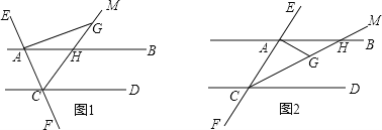
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“一带一路”国际合作高峰论坛在北京举行,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区.已知甲种商品的销售单价为900元,乙种商品的销售单价为600元.
(1)已知乙种商品的销售量不能低于甲种商品销售量的三分之一,则最多能销售甲种商品多少万件?
(2)在(1)的条件下,要使甲、乙两种商品的销售总收入不低于5700万元,请求甲种商品销售量的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD,点P是对角线AC所在直线上的动点,点E在BC边所在直线上, PE=PB.
(1)如图1,当点E在线段BC上时,
求证:①PE=PD,②PE⊥PD.
简析: 由正方形的性质,图1中有三对全等的三角形,
即△ABC≌△ADC,_______≌_______,和_______≌______,由全等三角形性质,结合条件中PE=PB,易证PE=PD.要证PE⊥PD,考虑到∠ECD = 90°,故在四边形PECD中,只需证∠PDC +∠PEC=______即可.再结合全等三角形和等腰三角形PBE的性质,结论可证.

(2)如图2,当点E在线段BC的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由;

(3)若AB=1,当△PBE是等边三角形时,请直接写出PB的长.

相关试题

