【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: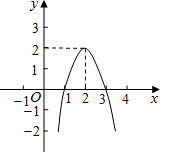
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c<0的解集;
(3)若方程ax2+bx+c+k=0有两个不相等的实数根,求k的取值范围.
参考答案:
【答案】
(1)解:如图,∵抛物线 ![]() 与
与 ![]() 轴两交点的横坐标分别为1和3,
轴两交点的横坐标分别为1和3,
∴方程 ![]() 的两根为
的两根为 ![]() ;
;
(2)解:如图,∵抛物线 ![]() 位于
位于 ![]() 轴下方部分图象所对应的自变量的取值范围为:
轴下方部分图象所对应的自变量的取值范围为: ![]() 或
或 ![]() ,
,
∴不等式 ![]() 的解集为:
的解集为: ![]() 或
或 ![]() ;
;
(3)解:如图,可知点(1,0)、(3,0)在抛物线上,
∴ 抛物线的解析式为 ![]() ,
,
又∵点(2,2)在抛物线上,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为 ![]() ,
,
所以方程 ![]() 可化为:
可化为: ![]() ,
,
∵该方程有两个不相等的实数根,
∴△= ![]() ,解得
,解得 ![]() .
.
【解析】(1)观察函数图像,可知抛物线与x轴交于两点,这两点的横坐标就是对应的函数值为0时的自变量的值,即方程ax2+bx+c=0的两个根。
(2)要求不等式ax2+bx+c<0的解集,就是要求y<0时自变量的取值范围,观察y<0的图像,就是看x轴下方的图像即可求出结果。
(3)先观察函数图像可知点(1,0)、(3,0)(2,2)在抛物线上,设函数解析式为交点式,求出函数解析式,得出 2 x 2 + 8 x 6 + k = 0 ,再由该方程有两个不相等的实数根,得出b2-4ac>0,建立不等式求解即可。
【考点精析】通过灵活运用求根公式和抛物线与坐标轴的交点,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.
-
科目: 来源: 题型:
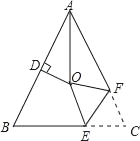
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=56°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】交警通常根据刹车后轮滑行的距离来测算车辆行驶的速度,所用的经验公式是u=16
 .其中u表示车速(单位:km/h),d表示刹车距离(单位:m),f表示摩擦系数.在一次交通事故中,测得d=20m,f=1.44,而发生交通事故的路段限速为80km/h,肇事汽车是否违规超速行驶?说明理由.(参考数据:
.其中u表示车速(单位:km/h),d表示刹车距离(单位:m),f表示摩擦系数.在一次交通事故中,测得d=20m,f=1.44,而发生交通事故的路段限速为80km/h,肇事汽车是否违规超速行驶?说明理由.(参考数据: ≈1.4,
≈1.4, ≈2.2)
≈2.2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于O点,OM⊥AB;
(1)若∠1=∠2,求∠NOD;
(2)若∠1=
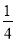 ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.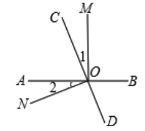
-
科目: 来源: 题型:
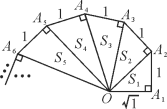
查看答案和解析>>【题目】细心观察图形,认真分析各式,然后解答问题.
OA22=(
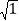 )2+1=2,S1=
)2+1=2,S1= ;
;OA32=12+(
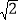 )2=3,S2=
)2=3,S2= ;
;OA42=12+(
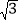 )2=4,S3=
)2=4,S3= ;…
;…(1)请用含有n(n为正整数)的等式表示上述变化规律:OAn2=________,Sn=________;
(2)若一个三角形的面积是2
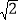 ,计算说明它是第几个三角形?
,计算说明它是第几个三角形?(3)求出S12+S22+S32+…+S92的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD;
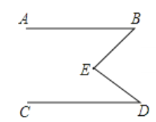
(1)你能找出∠B∠D∠BED的关系吗?
(2)如果∠B=46°,∠D=58°,则∠BED的度数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )

A. ①③ B. ②③ C. ①② D. ①②③
相关试题

