【题目】如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.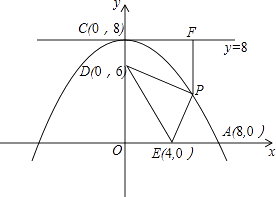
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.
参考答案:
【答案】
(1)解:设抛物线的解析式为y=ax2+8.
∵经过点A(8,0),
∴64a+8=0,解得a=﹣ ![]() .
.
抛物线的解析式为:y=﹣ ![]() x2+8
x2+8
(2)解:PD与PF的差是定值.
理由如下:设P(a,﹣ ![]() a2+8),则F(a,8),
a2+8),则F(a,8),
∵D(0,6),
∴PD= ![]() =
= ![]() =
= ![]() a2+2,PF=8﹣(
a2+2,PF=8﹣( ![]() )=
)= ![]() .
.
∴PD﹣PF=2.
(3)解:①当点P运动时,DE大小不变,则PE与PD的和最小时,△PDE的周长最小,
∵PD﹣PF=2,
∴PD=PF+2,
∴PE+PD=PE+PF+2,
∴当P、E、F三点共线时,PE+PF最小,此时点P,E的横坐标都为4,
∵将x=4代入y=﹣ ![]() x2+8,得y=6,
x2+8,得y=6,
∴P(4,6),此时△PDE的周长最小.
②如图1所示:过点P做PH⊥x轴,垂足为H.
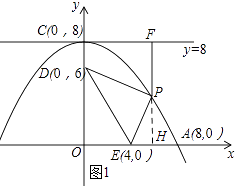
设P(a,﹣ ![]() a2+8)
a2+8)
∴PH=﹣ ![]() a2+8,EH=a﹣4,OH=a
a2+8,EH=a﹣4,OH=a
S△DPE=S梯形PHOD﹣S△PHE﹣S△DOE= ![]() a(﹣
a(﹣ ![]() a2+8+6)﹣
a2+8+6)﹣ ![]() (
( ![]() +8)(a﹣4)﹣
+8)(a﹣4)﹣ ![]() ×4×6=﹣
×4×6=﹣ ![]() a2+3a+4=﹣
a2+3a+4=﹣ ![]() (a﹣6)2+13.
(a﹣6)2+13.
∵点P是抛物线上点A,C间的一个动点(含端点),
∴0≤a≤8,
∴当a=6时,S△DPE取最大值为13.当a=0时,S△DPE取最小值为4.即4≤S△DPE≤13,其中,当S△DPE=12时,有两个点P.
∴共有11个令S△DPE为整数的点.
【解析】(1)此抛物线的顶点在y轴上,因此设此抛物线解析式为y=ax2+k,将点A、点B的坐标分别代入,就可求出函数解析式。
(2)抓住PF⊥直线y=8,设出点P、点F的坐标,用含a的代数式分别表示出PD、PF的长,再求出它们的差即可。
(3)①要使△PDE的周长最小,而DE的长是一个定值,关键是DP+PE的值要最小,由(2)可知PD=PF+2,即PE+PD=PE+PF+2,根据两点之间线段最短,P、E、F三点共线时,PE+PF最小,此时点P,E的横坐标都为4,代入函数解析式即可求出点P的坐标。②过点P做PH⊥x轴,垂足为H,设出点P的坐标,分别表示出PH、EH、的长,再求出S△DPE与a的函数关系式,根据点P是抛物线上点A,C间的一个动点(含端点),求出a的取值范围,继而求出S△DPE的取值范围,即可求出结果。
【考点精析】本题主要考查了二次函数的最值和勾股定理的概念的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE,CF和EF,则下列结论,一定成立的个数是( )
①△CDF≌△EBC;
②△CEF是等边三角形;
③∠CDF=∠EAF;
④CE∥DF

A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,四边形OABC为矩形,OA在x轴正半轴上,OC在y轴正半轴上,且A(10,0)、C(0,8)
(1)如图1,在矩形OABC的边AB上取一点E,连接OE,将△AOE沿OE折叠,使点A恰好落在BC边上的F处,求AE的长;
(2)将矩形OABC的AB边沿x轴负方向平移至MN(其它边保持不变),M、N分别在边OA、CB上且满足CN=OM=OC=MN.如图2,P、Q分别为OM、MN上一点.若∠PCQ=45°,求证:PQ=OP+NQ;
(3)如图3,S、G、R、H分别为OC、OM、MN、NC上一点,SR、HG交于点D.若∠SDG=135°,HG=4
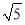 ,求RS的长.
,求RS的长.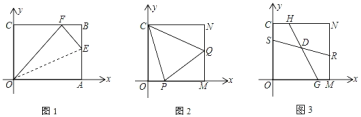
-
科目: 来源: 题型:
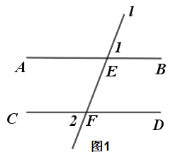
查看答案和解析>>【题目】已知:直线l分别交AB、CD与E、F两点,且AB∥CD.
(1) 说明:∠1=∠2;
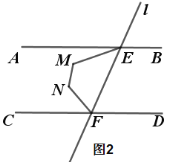
(2) 如图2,点M、N在AB、CD之间,且在直线l左侧,若∠EMN+∠FNM=260°,
①求:∠AEM+∠CFN的度数;
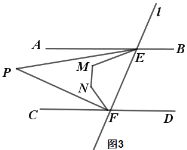
②如图3,若EP平分∠AEM,FP平分∠CFN,求∠P的度数;
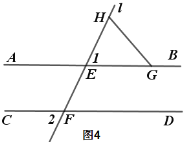
(3) 如图4,∠2=80°,点G在射线EB上,点H在AB上方的直线l上,点Q是平面内一点,连接QG、QH,若∠AGQ=18°,∠FHQ=24°,直接写出∠GQH的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板按如图①的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,得到如图②,测得CG=6
 ,则AC长是( )
,则AC长是( )
A.6+2
B.9
C.10
D.6+6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.李萌与和谢娜同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).

请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了 名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的所占圆心角的度数为 .
(4)根据调查结果,估算该校1800名学生中大约有多少人选择小组合作学习模式?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商城销售A、B两种型号的电风扇,进价分别为160元、120元,下表是近两周的销售情况:
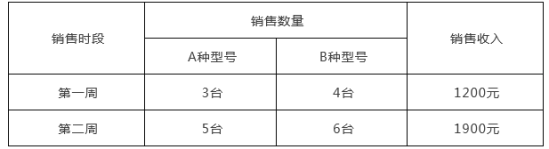
(1)求A、B两种型号的电风扇的销售单价;
(2)若商城准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商城要求至少购买A型电风扇35台,商场共有几种进货方案?并给出利润最大的方案?
相关试题

