【题目】为了解中学生的体能情况,某校抽取了50名八年级学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频数分布直方图如下图所示已知图中从左到右前第一、第二、第三、第五小组的频率分别为0.04 , 0.12 ,0.4 ,O.28 ,根据已知条件解答下列问题:
(1)第四个小组的频率是多少? 你是怎样得到的?
(2)这五小组的频数各是多少?
(3)在这次跳绳中,跳绳次数的中位数落在第几小组内?
(4)将频数分布直方图补全,并分别写出各个小组的频数,并画出频数分布折线图.

参考答案:
【答案】答案见解析
【解析】试题分析:(1)用1减去其余四组的频率即可;
(2)利用频数=频率乘总数得到;
(3)中位数是第25个同学、第26个同学跳绳次数之和的一半;
(4)依数画图即可.
试题解析:解:(1)由1减去已知4个小组的频率之和得到结果,第四个小组的频率=1﹣(0.04+0.12+0.4+0.28)=0.16;
(2)由频率=![]() ,且知各小组的频率分别为0.04,0.12,0.4,0.16,0.28及总人数为50,故有50×0.04=2,50×0.12=6,50×0.4=20,50×0.16=8,50×0.28=14,从而可知前5个小组的频数分别为2,6,20,8,14;
,且知各小组的频率分别为0.04,0.12,0.4,0.16,0.28及总人数为50,故有50×0.04=2,50×0.12=6,50×0.4=20,50×0.16=8,50×0.28=14,从而可知前5个小组的频数分别为2,6,20,8,14;
(3)由中位数应是第25个同学、第26个同学跳绳次数之和的一半.
由频数分布直方图可知,第25个同学、第26个同学跳绳次数均落在第三个小组内.
故而可知在这次测试中,跳绳次数的中位数落在第三小组内;
(4)由于第四小组的频数为8,第一小组频数为2,故第四小组的小长方形的高应是第一小组小长方形的高的4倍.
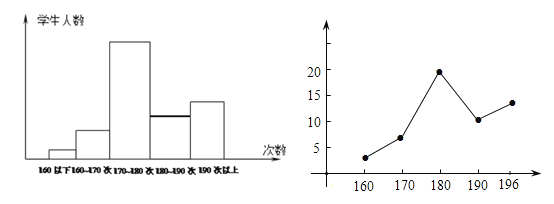
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)若∠AOC=30°,求∠DOE的度数;
(2)若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(3)在(1)的条件下,∠BOC的内部有一射线OG,射线OG将∠BOC分为1:4两部分,求∠DOG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC逆时针旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角∠A CA′的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】圆的内接等腰三角形ABC,圆的半径为10,如果底边BC的长为16,那么△ABC的面积为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;②△HED的面积是1﹣
 ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG= .其中正确的结论是( )
.其中正确的结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AB=CD,M、N分别是AD和BC的中点,延长BA和CD分别交射线NM于点E和点F,若tan∠F=
 , FC=FN,EN=
, FC=FN,EN= , 则EF=
, 则EF= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )

A. 1 B.
 ﹣1 C.
﹣1 C.  D. 2﹣
D. 2﹣
相关试题

