【题目】如图①,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)若∠AOC=30°时,则∠DOE的度数为_____;
(2)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
(3)将图①中的∠COD绕顶点O顺时针旋转至图③的位置,其他条件不变.直接写出∠AOC和∠DOE的度数之间的关系:_____.
参考答案:
【答案】 15° ∠AOC=360°﹣2∠DOE
【解析】试题分析:(1)由已知可求出∠BOC=180°-∠AOC=150°,再由∠COD是直角,OE平分∠BOC求出∠DOE的度数;
(2)由∠COD是直角,OE平分∠BOC可得出∠COE=∠BOE=90°-∠DOE,则得∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),从而得出∠AOC和∠DOE的度数之间的关系;
(3)根据(2)的解题思路,即可解答.
试题解析:(1)由已知得∠BOC=180°﹣∠AOC=150°,
又∠COD是直角,OE平分∠BOC,
∴∠DOE=∠COD﹣![]() ∠BOC=90°﹣
∠BOC=90°﹣![]() ×150°=15°;
×150°=15°;
(2)∠AOC=2∠DOE;
理由:∵∠COD是直角,OE平分∠BOC,
∴∠COE=∠BOE=90°﹣∠DOE,
则得∠AOC=180°﹣∠BOC=180°﹣2∠COE=180°﹣2(90°﹣∠DOE),
所以得:∠AOC=2∠DOE;
(3)∠AOC=360°﹣2∠DOE;
理由:∵OE平分∠BOC,
∴∠BOE=2∠COE,
则得∠AOC=180°﹣∠BOE=180°﹣2∠COE=180°﹣2(∠DOE﹣90°),
所以得:∠AOC=360°﹣2∠DOE;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B在双曲线y=
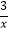 (x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线y=
(x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线y=  (x>0)上,此时OABC的面积为 .
(x>0)上,此时OABC的面积为 . 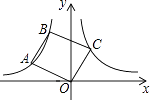
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人从
 地前往
地前往 地,甲的速度是每小时80千米,乙的速度是甲的速度的1.5倍,甲比乙早出发0.5小时,结果甲比乙晚到1.5小时.
地,甲的速度是每小时80千米,乙的速度是甲的速度的1.5倍,甲比乙早出发0.5小时,结果甲比乙晚到1.5小时.(1)求
 ,
, 两地的路程是多少千米?
两地的路程是多少千米?(2)当甲到达
 地后,乙再与甲同时从
地后,乙再与甲同时从 地按各自的原速返回
地按各自的原速返回 地,若他们由
地,若他们由 地返回
地返回 地的过程中所行走路程的和为180千米,则甲走了多少小时?
地的过程中所行走路程的和为180千米,则甲走了多少小时?(3)若乙到达
 地后立即按原速返回,问再经过多长时间甲与乙之间的距离为20千米?
地后立即按原速返回,问再经过多长时间甲与乙之间的距离为20千米? -
科目: 来源: 题型:
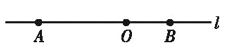
查看答案和解析>>【题目】如图,直线
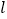 上有
上有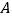 ,
, 两点,
两点, ,
, 是线段
是线段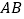 上的一点,
上的一点, .
.
(1)
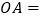
 ,
,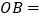
 ;
;(2)若点
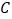 是直线
是直线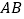 上一点,且满足
上一点,且满足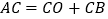 ,求
,求 的长;
的长;(3)若动点
 ,
, 分别从点
分别从点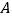 ,
, 同时出发,向右运动,点
同时出发,向右运动,点 的速度为
的速度为 ,点
,点 的速度为
的速度为 .设运动时间为
.设运动时间为 ,当点
,当点 与点
与点 重合时,
重合时, ,
, 两点停止运动.
两点停止运动.①当
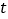 为何值时,
为何值时,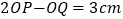 ?
?②当点
 经过点
经过点 时,动点
时,动点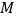 从点
从点 出发,以
出发,以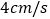 的速度也向右运动.当点
的速度也向右运动.当点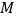 追上点
追上点 后立即返回,以
后立即返回,以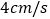 的速度向点
的速度向点 运动,遇到点
运动,遇到点 后再立即返回,以
后再立即返回,以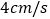 的速度向点
的速度向点 运动,如此往返.当点
运动,如此往返.当点 与点
与点 重合时,
重合时, ,
, 两点停止运动,此时点
两点停止运动,此时点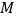 也停止运动.在此过程中,请直接写出点
也停止运动.在此过程中,请直接写出点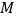 运动的总路程.
运动的总路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x、y的二元一次方程组
 的解都为正数.
的解都为正数.(1)求
 的取值范围;
的取值范围;(2)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).
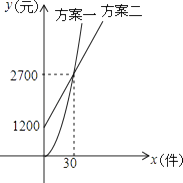
(1)分别求两种方案中y关于x的函数关系式;
(2)当销售达到多少件时,两种方案月报酬差额将达到3800元?
(3)若公司决定改进“方案二”:保持基本工资不变,每件报酬增加m元,使得当销售员销售产量达到40件时,两种方案的报酬差额不超过1000元.求m的取值范围.
相关试题

