【题目】某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).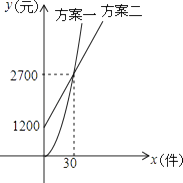
(1)分别求两种方案中y关于x的函数关系式;
(2)当销售达到多少件时,两种方案月报酬差额将达到3800元?
(3)若公司决定改进“方案二”:保持基本工资不变,每件报酬增加m元,使得当销售员销售产量达到40件时,两种方案的报酬差额不超过1000元.求m的取值范围.
参考答案:
【答案】
(1)解:设 ![]() ,把(30,2700)代入得:900a=2700,
,把(30,2700)代入得:900a=2700,
解得:a=3,
∴ ![]() .
.
设y2=kx+b,把(0,1200),(30,2700)代入得: ![]() ,
,
解得: ![]() ,
,
∴y2=50x+1200.
(2)解:由题意得:30x2﹣(50x+1200)=3800,
解得: ![]() =50,
=50, ![]() =
= ![]() (舍去),
(舍去),
答:当销售达到50件时,两种方案月报酬差额将达到3800元
(3)解:当销售员销售产量达到40件时,
方案一的月报酬为:(50+m)×40+1200=40m+3200,
方案二的月报酬为:3×402=4800,
由题意得:4800﹣(40m+3200)≤1000,且40m+3200﹣4800≤1000,
解得:15≤m≤65
【解析】(1)根据图像上的交点坐标(30,2700),得到二次函数和一次函数的解析式;(2)根据差额达到3800元,得到一元二次方程,得到当销售达到50件时,两种方案月报酬差额将达到3800元;(3)当销售员销售产量达到40件时,求出方案一和方案二的报酬,根据报酬差额不超过1000元,求出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)若∠AOC=30°时,则∠DOE的度数为_____;
(2)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
(3)将图①中的∠COD绕顶点O顺时针旋转至图③的位置,其他条件不变.直接写出∠AOC和∠DOE的度数之间的关系:_____.
-
科目: 来源: 题型:
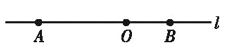
查看答案和解析>>【题目】如图,直线
 上有
上有 ,
, 两点,
两点, ,
, 是线段
是线段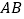 上的一点,
上的一点, .
.
(1)
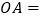
 ,
,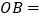
 ;
;(2)若点
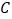 是直线
是直线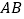 上一点,且满足
上一点,且满足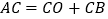 ,求
,求 的长;
的长;(3)若动点
 ,
, 分别从点
分别从点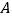 ,
, 同时出发,向右运动,点
同时出发,向右运动,点 的速度为
的速度为 ,点
,点 的速度为
的速度为 .设运动时间为
.设运动时间为 ,当点
,当点 与点
与点 重合时,
重合时, ,
, 两点停止运动.
两点停止运动.①当
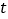 为何值时,
为何值时,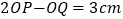 ?
?②当点
 经过点
经过点 时,动点
时,动点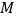 从点
从点 出发,以
出发,以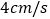 的速度也向右运动.当点
的速度也向右运动.当点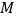 追上点
追上点 后立即返回,以
后立即返回,以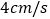 的速度向点
的速度向点 运动,遇到点
运动,遇到点 后再立即返回,以
后再立即返回,以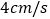 的速度向点
的速度向点 运动,如此往返.当点
运动,如此往返.当点 与点
与点 重合时,
重合时, ,
, 两点停止运动,此时点
两点停止运动,此时点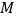 也停止运动.在此过程中,请直接写出点
也停止运动.在此过程中,请直接写出点 运动的总路程.
运动的总路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x、y的二元一次方程组
 的解都为正数.
的解都为正数.(1)求
 的取值范围;
的取值范围;(2)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.
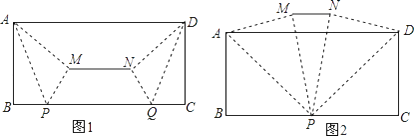
(1)【规律探索】请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
(2)【解决问题】如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

相关试题

