【题目】如图,点A、B在双曲线y= ![]() (x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线y=
(x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线y= ![]() (x>0)上,此时OABC的面积为 .
(x>0)上,此时OABC的面积为 . 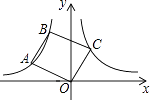
参考答案:
【答案】2 ![]()
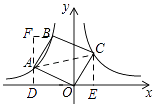
【解析】解:如图,连接AC,过A作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,则△ABF≌△COE,
设A(a,﹣ ![]() ),C(b,
),C(b, ![]() ),则OE=BF=b,CE=AF=
),则OE=BF=b,CE=AF= ![]() ,
,
∴B(a+b,﹣ ![]() +
+ ![]() ),
),
又∵点B在双曲线y= ![]() (x<0)上,
(x<0)上,
∴(a+b)(﹣ ![]() +
+ ![]() )=﹣3,
)=﹣3,
∴ ![]() ﹣
﹣ ![]() =2,
=2,
设 ![]() =x,则方程
=x,则方程 ![]() ﹣
﹣ ![]() =2可化为3x﹣
=2可化为3x﹣ ![]() =2,
=2,
解得x= ![]() 或x=
或x= ![]() (舍去),
(舍去),
∴ ![]() =
= ![]() ,
, ![]() =﹣
=﹣ ![]() ,
,
∴平行四边形OABC的面积=2×S△OAC
=2(S梯形ADEC﹣S△AOD﹣S△COE)
=2[ ![]() (﹣
(﹣ ![]() +
+ ![]() )(b﹣a)﹣
)(b﹣a)﹣ ![]() ×|﹣3|﹣
×|﹣3|﹣ ![]() ×|2|]
×|2|]
=﹣ ![]() +3+2﹣
+3+2﹣ ![]() ﹣5
﹣5
=﹣3× ![]() ﹣2×(﹣
﹣2×(﹣ ![]() )
)
=2 ![]() .
.
所以答案是:2 ![]() .
.
【考点精析】认真审题,首先需要了解比例系数k的几何意义(几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积),还要掌握平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.

(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为8,tan∠C= ,求线段AB的长,sin∠ADB的值.
,求线段AB的长,sin∠ADB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简
(1)
 ; (2)(﹣2a2)(3ab2﹣5ab3)
; (2)(﹣2a2)(3ab2﹣5ab3)(3)(x+3)(x﹣7)﹣x(x﹣1). (4)(a﹣2b+1)(a+2b+1)
(5)(3a﹣b)2﹣(2a+b)2﹣5a(a﹣b) (6)(x+2y)2(x﹣2y)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人从
 地前往
地前往 地,甲的速度是每小时80千米,乙的速度是甲的速度的1.5倍,甲比乙早出发0.5小时,结果甲比乙晚到1.5小时.
地,甲的速度是每小时80千米,乙的速度是甲的速度的1.5倍,甲比乙早出发0.5小时,结果甲比乙晚到1.5小时.(1)求
 ,
, 两地的路程是多少千米?
两地的路程是多少千米?(2)当甲到达
 地后,乙再与甲同时从
地后,乙再与甲同时从 地按各自的原速返回
地按各自的原速返回 地,若他们由
地,若他们由 地返回
地返回 地的过程中所行走路程的和为180千米,则甲走了多少小时?
地的过程中所行走路程的和为180千米,则甲走了多少小时?(3)若乙到达
 地后立即按原速返回,问再经过多长时间甲与乙之间的距离为20千米?
地后立即按原速返回,问再经过多长时间甲与乙之间的距离为20千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)若∠AOC=30°时,则∠DOE的度数为_____;
(2)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
(3)将图①中的∠COD绕顶点O顺时针旋转至图③的位置,其他条件不变.直接写出∠AOC和∠DOE的度数之间的关系:_____.
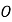
-
科目: 来源: 题型:
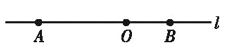
查看答案和解析>>【题目】如图,直线
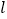 上有
上有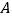 ,
, 两点,
两点, ,
, 是线段
是线段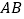 上的一点,
上的一点, .
.
(1)
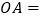
 ,
,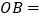
 ;
;(2)若点
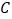 是直线
是直线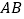 上一点,且满足
上一点,且满足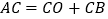 ,求
,求 的长;
的长;(3)若动点
 ,
, 分别从点
分别从点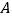 ,
, 同时出发,向右运动,点
同时出发,向右运动,点 的速度为
的速度为 ,点
,点 的速度为
的速度为 .设运动时间为
.设运动时间为 ,当点
,当点 与点
与点 重合时,
重合时, ,
, 两点停止运动.
两点停止运动.①当
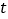 为何值时,
为何值时,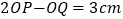 ?
?②当点
 经过点
经过点 时,动点
时,动点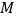 从点
从点 出发,以
出发,以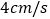 的速度也向右运动.当点
的速度也向右运动.当点 追上点
追上点 后立即返回,以
后立即返回,以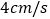 的速度向点
的速度向点 运动,遇到点
运动,遇到点 后再立即返回,以
后再立即返回,以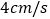 的速度向点
的速度向点 运动,如此往返.当点
运动,如此往返.当点 与点
与点 重合时,
重合时, ,
, 两点停止运动,此时点
两点停止运动,此时点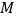 也停止运动.在此过程中,请直接写出点
也停止运动.在此过程中,请直接写出点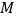 运动的总路程.
运动的总路程.
相关试题

