【题目】如图,在平面直角坐标系中有一正方形AOBC,反比例函数y= ![]() 经过正方形AOBC对角线的交点,半径为(6﹣3
经过正方形AOBC对角线的交点,半径为(6﹣3 ![]() )的圆内切于△ABC,则k的值为 .
)的圆内切于△ABC,则k的值为 . 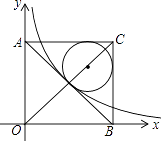
参考答案:
【答案】9
【解析】解:设正方形对角线交点为D,过点D作DM⊥AO于点M,DN⊥BO于点N,设圆心为Q,切点为H、E,连接QH、QE. 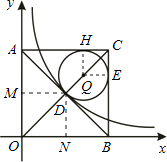
∵在正方形AOBC中,反比例函数y= ![]() 经过正方形AOBC对角线的交点,
经过正方形AOBC对角线的交点,
∴AD=BD=DO=CD,NO=DN,HQ=QE,HC=CE,
∵QH⊥AC,QE⊥BC,∠ACB=90°,
∴四边形HQEC是正方形.
∵半径为(6﹣3 ![]() )的圆内切于△ABC,
)的圆内切于△ABC,
∴DO=CD.
∵HQ2+HC2=QC2 ,
∴2HQ2=QC2=2×(6﹣3 ![]() )2 ,
)2 ,
∴QC2=108﹣72 ![]() =(6
=(6 ![]() ﹣6)2 ,
﹣6)2 ,
∴QC=6 ![]() ﹣6,
﹣6,
∴CD=6 ![]() ﹣6+(6﹣3
﹣6+(6﹣3 ![]() )=3
)=3 ![]() ,
,
∴DO=3 ![]() .
.
∵NO2+DN2=DO2=(3 ![]() )2=18,
)2=18,
∴2NO2=18,
∴NO2=9,
∴DNNO=9,
即:xy=k=9.
所以答案是9.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形),还要掌握三角形的内切圆与内心(三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q
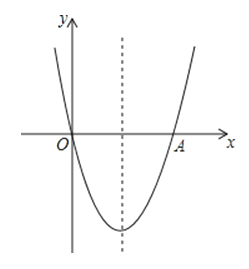
(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 .
(2)若两个三角形面积满足S△POQ= S△PAQ , 求m的值
S△PAQ , 求m的值
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP , 其中正确的个数是( )
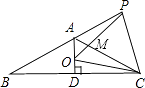
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,H,G,N在同一直线上,△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边.已知EF=2.1 cm,EH=1.1 cm,HN=3.3 cm.
(1)写出其他对应边及对应角;
(2)求线段MN及线段HG的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB,用尺规作∠ABC=90°,作法如下:
小明的作法:(1)分别以A、B为圆心AB长为半径画弧,两弧交于点P;(2)以P为圆心,AB长为半径画弧交AP的延长线于C;连接AC,则∠ABC=90°

(1)请证明∠ABC=90°;
(2)请你用不同的方法,用尺规作∠ABC=90°.
(要求:保留作图痕迹,不写作法,并用2B铅笔把作图痕迹描粗)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中是中心对称图形的是
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|1﹣
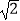 |+(π﹣2014)0﹣2sin45°+(
|+(π﹣2014)0﹣2sin45°+(  )﹣2 .
)﹣2 .
相关试题

