【题目】如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 的一个外角,根据要求进行尺规作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
的一个外角,根据要求进行尺规作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
(1)作![]() 的平分线
的平分线![]() .
.
(2)作线段![]() 的垂直平分线,与
的垂直平分线,与![]() 交于点
交于点![]() ,与
,与![]() 边交于点
边交于点![]() ,判断线段
,判断线段![]() 是否也被
是否也被![]() 垂直平分,并说明理由.
垂直平分,并说明理由.
参考答案:
【答案】(1)见解析(2)见解析;线段![]() 被
被![]() 垂直平分(从三角形全等出发)
垂直平分(从三角形全等出发)
【解析】
(1)如图,由基本作图作AM平分∠DAB;
(2)根据等腰三角形的性质得∠B=∠C,由角平分线的定义得∠DAM=∠BAM,则根据三角形外角性质得到∠BAM=∠B,再根据线段垂直平分线的性质得到EA=EB,则∠B=∠EAB,所以∠BAM=∠EAB,从而得到EO=FO,即AB垂直平分EF.
(1)如图,AM为所作;
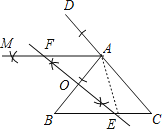
(2)段EF被AB垂直平分.理由如下:
∵AB=AC,
∴∠B=∠C,
∵AM平分∠DAB,
∴∠DAM=∠BAM,
∵∠DAM+∠BAM=∠B+∠C,
∴∠BAM=∠B,
∵EF垂直平分AB,
∴EA=EB,
∴∠B=∠EAB,
∴∠BAM=∠EAB,
而AB⊥EF,
∴EO=FO,
∴AB垂直平分EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,P是BC上一点,E是AB上一点,PD平分∠APC,PE⊥PD,连接DE交AP于F,在以下判断中,不正确的是( )

A.当P为BC中点,△APD是等边三角形
B.当△ADE∽△BPE时,P为BC中点
C.当AE=2BE时,AP⊥DE
D.当△APD是等边三角形时,BE+CD=DE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,
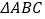 的顶点
的顶点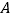 的坐标为
的坐标为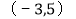 ,顶点
,顶点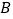 的坐标为
的坐标为 ,顶点
,顶点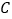 的坐标为
的坐标为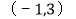 .
.(1)请你在所给的平面直角坐标系中,画出
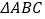 关于
关于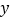 轴对称的
轴对称的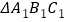 ;
;(2)将(1)中得到的
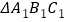 向下移动4个单位得到
向下移动4个单位得到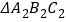 ,画出
,画出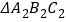 ;
;(3)在
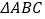 中有一点
中有一点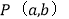 ,直接写出经过以上两次图形变换后
,直接写出经过以上两次图形变换后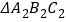 中对应点
中对应点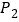 的坐标.
的坐标.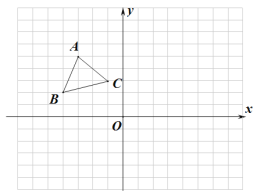
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,一次函数
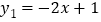 的图象与
的图象与 轴交于点
轴交于点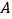 .
.(1)若点
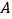 关于
关于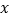 轴的对称点
轴的对称点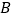 在一次函数
在一次函数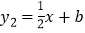 的图象上,求
的图象上,求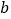 的值;
的值;(2)求由直线
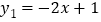 ,(1)中的直线
,(1)中的直线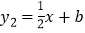 以及
以及 轴围成的三角形的面积.
轴围成的三角形的面积.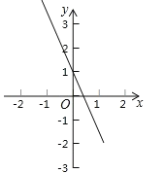
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)

-
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始,连续的偶数相加,它们和的情况如表:
加数的个数n
S
1
2=1×2
2
2+4=6=2×3
3
2+4+6=15=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
(1)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=;
(2)如下数表是由从1开始的连续自然数组成,观察规律:
①第n行的第一个数可用含n的式子表示为; -
科目: 来源: 题型:
查看答案和解析>>【题目】某校在学习贯彻十九大精神“我学习,我践行”的活动中,计划组织全校1300名师生到林业部门规划的林区植树,经研究,决定租用当地出租车公司提供的
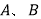 两种型号的客车共50辆作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量与租车信息:
两种型号的客车共50辆作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量与租车信息:型号
载客量
租金单价
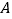
30人/辆
300元/辆
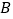
20人/辆
240元/辆
注:载客量指的是每辆车客车最多可载该校师生的人数
(1)设租用
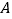 型号客车
型号客车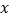 辆,租车总费用
辆,租车总费用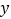 元,求
元,求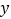 与
与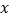 的函数解析式,并直接写出
的函数解析式,并直接写出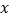 的取值范围;
的取值范围;(2)若要使租车总费用不超过13980元,一共有几种租车方案?哪种租车方案最省钱?
相关试题

