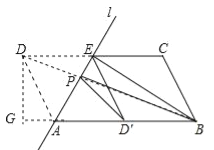
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形,根据折叠的性质得到AD=AD′,然后又菱形的判定定理即可得到结论;(2)由四边形DAD′E是平行四边形,得到DAD′E是菱形,推出D与D′关于AE对称,连接BD交AE于P,则BD的长即为PD′+PB的最小值,过D作DG⊥BA于G,解直角三角形得到AG=![]() ,DG=
,DG=![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
试题解析:(1)证明:∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴CE=D′B,CE∥D′B,
∴四边形BCED′是平行四边形;
∵AD=AD′,
∴DAD′E是菱形,
(2)∵四边形DAD′E是菱形,
∴D与D′关于AE对称,
连接BD交AE于P,则BD的长即为PD′+PB的最小值,
过D作DG⊥BA于G,
∵CD∥AB,
∴∠DAG=∠CDA=60°,
∵AD=1,
∴AG=![]() ,DG=
,DG=![]() ,
,
∴BG=![]() ,
,
∴BD=![]() =
=![]() ,
,
∴PD′+PB的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
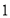 个单位长度的小正方形组成的网格中,
个单位长度的小正方形组成的网格中,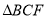 、正方形
、正方形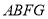 、正方形
、正方形 的顶点均在格点上.
的顶点均在格点上.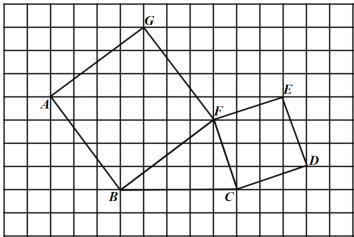
(1)以格点为原点,建立合适的平面直角坐标系,使得
 、
、 坐标分别为
坐标分别为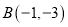 、
、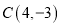 ,则点
,则点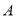 的坐标为______,点
的坐标为______,点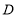 的坐标为_______;
的坐标为_______;(2)利用面积计算线段
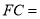 ________;
________;(3)点
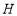 为直线
为直线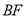 上一动点,求
上一动点,求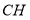 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.
(1)若∠DBC=30°,求∠A的度数;
(2)若点F在线段AE上,且7∠DBC-2∠ABF=180°,请问图中是否存在与∠DFB相等的角?若存在,请写出这个角,并说明理由;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图①为北斗七星的位置图,图②将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.
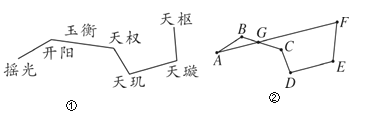
(1)求∠F的度数;
(2)计算∠B-∠CGF的度数是______;(直接写出结果)
(3)连接AD,∠ADE与∠CGF满足怎样数量关系时,BC∥AD,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B、C是⊙A上的两点,AB的垂直平分线与⊙A交于E、F两点,与线段AC交于D点.若∠BFC=20°,则∠DBC=( )

A.30°
B.29°
C.28°
D.20° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,
, .
.

备用图
(1)直接写出
 _________;
_________;(2)已知点
 ,满足
,满足 ,求
,求 的值;
的值;(3)如图,把直线
 以每秒
以每秒 个单位长度的速度向右平移,求平移多少秒时该直线恰好经过
个单位长度的速度向右平移,求平移多少秒时该直线恰好经过 点.
点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个多位正整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”.例如:49与76,因为4+9=7+6=13,所以49与76互为“调和数”;又如:225与18,因为2+2+5=1+8=9,所以225与18互为“调和数”.
(1)362与________互为“调和数”(写出一个即可);
(2)若两位数
 与75是一对“调和数”,且
与75是一对“调和数”,且 的十位数字是个位数字的2倍,求
的十位数字是个位数字的2倍,求 的值.
的值.
相关试题

