【题目】如图,在边长为![]() 个单位长度的小正方形组成的网格中,
个单位长度的小正方形组成的网格中,![]() 、正方形
、正方形![]() 、正方形
、正方形![]() 的顶点均在格点上.
的顶点均在格点上.
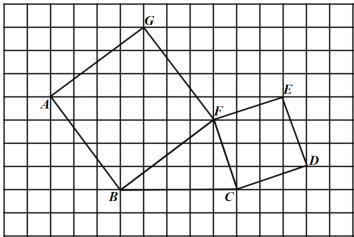
(1)以格点为原点,建立合适的平面直角坐标系,使得![]() 、
、![]() 坐标分别为
坐标分别为![]() 、
、![]() ,则点
,则点![]() 的坐标为______,点
的坐标为______,点![]() 的坐标为_______;
的坐标为_______;
(2)利用面积计算线段![]() ________;
________;
(3)点![]() 为直线
为直线![]() 上一动点,求
上一动点,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;(3)3
;(3)3
【解析】
(1)根据点B、C的坐标可知坐标原点的位置,由此得到点A、D的坐标;
(2)根据面积的和差即可得出FC的平方,进而可求得FC的长.
(3)根据垂线段最短可知当CH⊥BF时,CH最短,再利用面积法即可求得CH的最小值.
解:(1)平面直角坐标系如图所示,

此时点A的坐标为(﹣4,1),点D的坐标为(7,﹣2).
(2)如图,

由图形可知:△FNC≌△CPD≌△DQE≌△EMF,
∴S正方形FCDE=S正方形MNPQ﹣4S△FNC=42﹣4×![]() ×3×1=10=FC2,
×3×1=10=FC2,
∴FC=![]() ;
;
(3)解:如图,过点C作![]() 时,由题意可知,此时的
时,由题意可知,此时的![]() 有最小值,
有最小值,

由图可知:![]() ,
,![]() ,
,
![]() ,
,
 .
.
![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,横、纵坐标都为整数的点称为整点.如图,从内向外依次为第
 ,
, ,
, ,
, ,
, 个正方形(实线),若整点
个正方形(实线),若整点 在第
在第 个正方形的边上,则
个正方形的边上,则 ,
, ,
, 之间满足的数量关系为_______.
之间满足的数量关系为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,分别把两个边长为
 的小正方形沿一条对角线裁成
的小正方形沿一条对角线裁成 个小三角形拼成一个大正方形,则大正方形的边长为_______
个小三角形拼成一个大正方形,则大正方形的边长为_______ ;
;
(2)若一个圆的面积与一个正方形的面积都是
 ,设圆的周长为
,设圆的周长为 ,正方形的周长为
,正方形的周长为 ,则
,则 _____
_____ (填“
(填“ ”或“
”或“ ”或“
”或“ ”号);
”号);(3)如图,若正方形的面积为
 ,李明同学想沿这块正方形边的方向裁出一块面积为
,李明同学想沿这块正方形边的方向裁出一块面积为 的长方形纸片,使它的长和宽之比为
的长方形纸片,使它的长和宽之比为 ,他能裁出吗?请说明理由?
,他能裁出吗?请说明理由?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A.24m
B.25m
C.28m
D.30m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.
(1)若∠DBC=30°,求∠A的度数;
(2)若点F在线段AE上,且7∠DBC-2∠ABF=180°,请问图中是否存在与∠DFB相等的角?若存在,请写出这个角,并说明理由;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图①为北斗七星的位置图,图②将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.
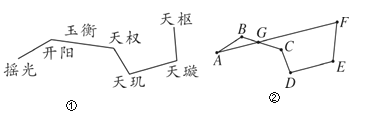
(1)求∠F的度数;
(2)计算∠B-∠CGF的度数是______;(直接写出结果)
(3)连接AD,∠ADE与∠CGF满足怎样数量关系时,BC∥AD,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

相关试题

