【题目】已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
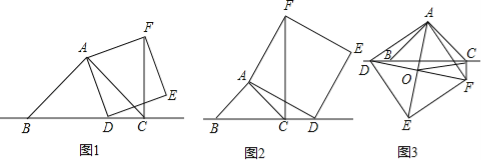
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)CF=BC+CD;(3)①CF=CD-BC;②△AOC是等腰三角形.理由见解析.
【解析】试题分析:(1)、①、根据等腰直角的性质得出∠ABC=∠ACB=45°,从而得出四边形ADEF是正方形,根据∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°得出∠BAD=∠CAF,从而得出△BAD和△CAF全等,则∠ACF=∠ABD=45°,从而得出垂直;②、根据 全等得出BD=CF,从而得出结论;(2)、根据(1)的证法的采购员BD=CF,得出CF=BC+CD;(3)、①、根据(1)的证法得出BD=CF,从而得出CF=CD-BC;②、∠BAC=90°,AB=AC得出∠ABD=135°,根据四边形ADEF是正方形得出∠BAC=∠BAF+∠CAF=90°,∠DAF=∠BAD+∠BAF=90°,从而得出△BAD和△CAF全等,则∠ACF=135°,从而得出∠FCD=∠ACF-∠ACB=90°,得出△FCD为直角三角形,根据正方形的性质得出OC=OA,从而说明△FCD为等腰直角三角形.
试题解析:(1)、①、∵∠BAC=90°,AB=AC, ∴∠ABC=∠ACB=45°, ∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°, ∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°, ∴∠BAD=∠CAF,
在△BAD和△CAF中, AB=AC ∠BAD=∠CAF AD=AF ∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°, ∴∠ACF+∠ACB=90°, ∴BD⊥CF;
②、由①△BAD≌△CAF可得BD=CF, ∵BD=BC-CD, ∴CF=BC-CD;
(2)、与(1)同理可得BD=CF, 所以,CF=BC+CD;
(3)、①、与(1)同理可得,BD=CF, 所以,CF=CD-BC;
②∵∠BAC=90°,AB=AC, ∴∠ABC=∠ACB=45°, 则∠ABD=180°-45°=135°,
∵四边形ADEF是正方形, ∴AD=AF,∠DAF=90° ∵∠BAC=∠BAF+∠CAF=90°,∠DAF=∠BAD+∠BAF=90°,
∴∠BAD=∠CAF, 在△BAD和△CAF中,AB=AC ∠BAD=∠CAF AD=AF ∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=180°-45°=135°, ∴∠FCD=∠ACF-∠ACB=90°,则△FCD为直角三角形,
∵正方形ADEF中,O为DF中点, ∴OC=![]() DF ∵在正方形ADEF中,OA=
DF ∵在正方形ADEF中,OA=![]() AEAE=DF, ∴OC=OA,
AEAE=DF, ∴OC=OA,
∴△AOC是等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课中,小辉将边长为
 和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.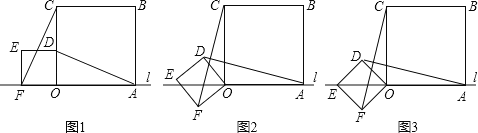
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣2,3),B(﹣3,2),C(﹣1,1).

(1)画出△ABC关于原点O对称的△A1B1C1;
(2)若将△ABC绕点C顺时针方向旋转90°后,求AC边扫过的图形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅不完整的统计图,请根据图中信息,解答下列问题:

(1)求扇形统计图中m的值;
(2)补全条形统计图;
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排
 人,问学校开设多少个“实践活动类”课程的班级比较合理?
人,问学校开设多少个“实践活动类”课程的班级比较合理? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为开展体育大课间活动,需要购买篮球与足球若干个.已知购买2个篮球和3个足球共需要380元;购买4个篮球和5个足球共需要700元.
(1)求购买一个篮球、一个足球各需多少元;
(2)若体育老师带了8000元去购买这种篮球与足球共100个.由于数量较多,店主给出“一律打九折”的优惠价,那么他最多能购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线MN交⊙O于A,B两点,AC是⊙O的直径,DE与⊙O相切于点D,且DE⊥MN于点E. 求证:AD平分∠CAM.

相关试题

