【题目】如图,直线MN交⊙O于A,B两点,AC是⊙O的直径,DE与⊙O相切于点D,且DE⊥MN于点E. 求证:AD平分∠CAM.
参考答案:
【答案】证明:连接OD,如图所示: ∵DE与⊙O相切于D,
∴OD⊥DE,
又∵DE⊥MN,
∴OD∥MN,
∴∠ODA=∠DAE,
又∵OD=OA,
∴∠ODA=∠OAD,
∴∠OAD=∠DAE,
∴AD平分∠CAM.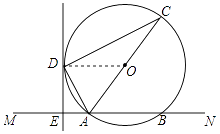
【解析】连接OD,由DE与⊙O相切于D,得到OD⊥DE,又因为DE⊥MN,推出OD∥MN,得到内错角∠ODA=∠DAE,由等腰三角形的性质得到∠ODA=∠OAD,于是推出∠OAD=∠DAE,即可得出AD平分∠CAM.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
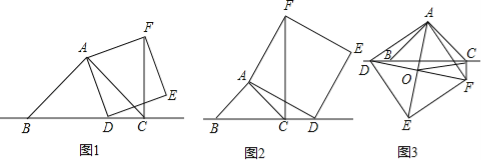
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅不完整的统计图,请根据图中信息,解答下列问题:

(1)求扇形统计图中m的值;
(2)补全条形统计图;
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排
 人,问学校开设多少个“实践活动类”课程的班级比较合理?
人,问学校开设多少个“实践活动类”课程的班级比较合理? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为开展体育大课间活动,需要购买篮球与足球若干个.已知购买2个篮球和3个足球共需要380元;购买4个篮球和5个足球共需要700元.
(1)求购买一个篮球、一个足球各需多少元;
(2)若体育老师带了8000元去购买这种篮球与足球共100个.由于数量较多,店主给出“一律打九折”的优惠价,那么他最多能购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=60°,点P为BC边上一点,设BP=x,AP2=y(如图1),已知y是x的二次函数的一部分,其图象如图2所示,点Q(2,12)是图象上的最低点.

(1)边AB= , BC边上的高AH=;
(2)当△ABP为直角三角形时,BP的长是多少. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE.

(1)求证:BN=AN;
(2)猜想线段CD与DE的数量关系,并说明理由.
相关试题

