【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第四象限,直线BD与反比例函数![]() 的图象交于点B、E.
的图象交于点B、E.
(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标;
(3)连结![]() 、
、![]() 、
、![]() ,求△
,求△![]() 的面积.
的面积.

参考答案:
【答案】(1)反比例函数解析式: ![]() ,直线BD的解析式:
,直线BD的解析式: ![]() ;(2)E(-2,1);(3)4.
;(2)E(-2,1);(3)4.
【解析】试题分析:(1)根据正方形的边长,正方形关于y轴对称,可得点A、B、D的坐标,根据待定系数法,可得函数解析式;
(2)根据两个函数解析式,可的方程组,根据解方程组,可得答案.
(3)如图,连接EC,求出EC的解析式为y=-3x-5,再求出直线与x轴的交点P的坐标(![]() ,0),分别求出ΔEPA和ΔCPA的面积即可得解.
,0),分别求出ΔEPA和ΔCPA的面积即可得解.
试题解析:(1)边长为2的正方形ABCD关于y轴对称,边在AD在x轴上,点B在第四象限,C在第三象限,
∴A(1,0),D(-1,0),B(1,-2),C(1-,-2).
∵反比例函数y=![]() 的图象过点B,
的图象过点B,
∴![]() =-2,k=-2,
=-2,k=-2,
∴反比例函数解析式为y=-![]() ,
,
设直线BD的解析式为y=kx+b,
∴![]() ,解得
,解得![]() .
.
直线BD的解析式y=-x-1;
(2)∵直线BD与反比例函数y=![]() 的图象交于点E,
的图象交于点E,
∴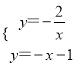 ,解得
,解得![]() 或
或![]() ,
,
∵B(1,-2),
∴E(-2,1).
(3)连接EC交x轴于点P,设EC所在的直线解析式为:y=kx+b,则有: ![]()
解得: ![]()
故EC所在直线解析式为:y=-3x-5.
当y=0时,x=-![]()
∴AP=![]()
∴SΔEAC=SΔEPA+SΔCPA=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的反比例函数,下表给出了x与y的一些值:

(1)写出这个反比例函数表达式;
(2)将表中空缺的x、y值补全.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
 的两根为
的两根为 、
、 ,且
,且 >
> ,求下列各式的值:
,求下列各式的值:(1)
 +
+  ;(2)
;(2) ;
;(3)
 ;(4)
;(4) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图9,正方形
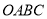 的面积为4,反比例函数(
的面积为4,反比例函数( )的图象经过点.
)的图象经过点.(1) 求点B的坐标和
 的值;
的值;(2) 将正方形分别沿直线
 、翻折,得到正方形
、翻折,得到正方形 、.设线段
、.设线段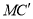 、分别与函数
、分别与函数 ()的图象交于点
()的图象交于点 、,求直线EF的解析式.
、,求直线EF的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/时;④乙先到达B地.其中正确的是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b 的图象与反比例函数y=
 的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:
的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:(1)一次函数的解析式;
(2)△AOB的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=y1+y2,y1与x+1成正比例,y2与x+1成反比例,当x=0时,y=﹣5;当x=2时,y=﹣7.
(1)求y与x的函数关系式;
(2)当y=5时,求x的值.
相关试题

