搜索
【题目】如图，直线l1：y1=2x+2与直线 l2：y2=mx+8相交于点 P（2，b）．
（1）求 b，m 的值；
（2）直接写出当 y1＜y2 时，自变量 x 的取值范围．
参考答案：
【答案】（1）b=6，m=-1；（2）x＜2
【解析】
(1) 把P（2，b）代入y1=2x+2上，即可求出b，再求m的值即可；
(2)观察图象写出直线y=2x+2的图象在直线y=x+8的图象的下方的自变量的取值范围即可；
⑴解：∵P为l1与l2的交点，
∴P（2，b）在y1=2x+2上，即b=2×2＋2=6．
∴P（2，6）．
∵P（2，6）在y2=mx+8上，
∴2m+8=6，m=-1．
∴b=6，m=-1．
⑵观察图象可知：当y1＜y2时x的取值范围x＜2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，四边形ABCD是正方形，点P在直线BC上，点G在直线AD上（P、G不与正方形顶点重合，且在CD的同侧），PD=PG，DF⊥PG于点H，交直线AB于点F，将线段PG绕点P逆时针旋转90°得到线段PE，连结EF．
（1）如图1，当点P与点G分别在线段BC与线段AD上时．
①求证：DG=2PC；
②求证：四边形PEFD是菱形；
（2）如图2，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD是怎样的特殊四边形，并证明你的猜想．
-
科目： 来源： 题型：
查看答案和解析>>【题目】菱形 ABCD 的对角线 AC=4，BD=2，以 AC 为边作正方形 ACEF，则 BF 的长为_____．
-
科目： 来源： 题型：
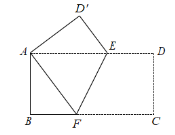
查看答案和解析>>【题目】如图，把一张长方形纸片 ABCD 折叠起来，使其对角顶点 A，C 重合，若其长 BC 为 9，宽 AB 为 3．
⑴求证：△AEF 是等腰三角形；
⑵EF= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某篮球队对队员进行定点投篮测试，每人每天投篮10次，现对甲、乙两名队员在五天中进球数（单位：个）进行统计，结果如下：
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算，甲进球的平均数为8，方差为3.2.
（1）求乙进球的平均数和方差；
（2）如果综合考虑平均成绩和成绩稳定性两方面的因素，从甲、乙两名队员中选出一人去参加定点投篮比赛，应选谁？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一个点在第一象限及x轴、y轴上移动，在第一秒钟，它从原点移动到点(1，0)，然后按照图中箭头所示方向移动，即(0，0)→(1，0)→(1，1)→)(0，1)→(0，2)→……，且每秒移动一个单位，那么第2018秒时，点所在位置的坐标是( ).
A. (6，44)B. (38，44)C. (44，38)D. (44，6)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线
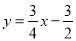与抛物线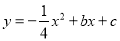
交于A、B两点，点A在x轴上，点B的横坐标为－8．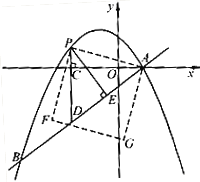
（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E．
①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的最大值；
②连接PA，以PA为边作如图所示一侧的正方形APFG．随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，求出对应的点P的坐标．
相关试题
