【题目】如图,等边△ABC的边长为2,CD为AB边上的中线,E为线段CD上的动点,以BE为边,在BE左侧作等边△BEF,连接DF,则DF的最小值为_____.

参考答案:
【答案】![]()
【解析】
连接AF,由等边三角形的性质可证△ABF≌△CBE,可得∠BAF=∠BCE=30°,即当DF⊥AF时,DF的值最小,由直角三角形的性质可求DF的最小值.
解:如图,连接AF,

∵△ABC是等边三角形,CD为AB边上的中线,
∴AB=BC=2,AD=BD=1,∠ABC=∠ACB=60°,∠BCE=30°,
∵△BEF是等边三角形
∴BF=BE,∠FBE=60°
∴∠FBE=∠ABC,
∴∠ABF=∠CBE,且AB=BC,BF=BE,
∴△ABF≌△CBE(SAS)
∴∠BAF=∠BCE=30°,
∴当DF⊥AF时,DF的值最小,
此时,∠AFD=90°,∠FAB=30°,
∴AD=2DF
∴DF的最小值为![]()
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点
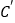 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( ) 
A. 80°B. 90°
C. 100°D. 110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数a使得关于x的不等式组
 ,有且仅有四个整数解,且使关于y的分式方程
,有且仅有四个整数解,且使关于y的分式方程 =1有整数解,则所有满足条件的整数a的值之和是( )
=1有整数解,则所有满足条件的整数a的值之和是( )A. 3B. 2C. ﹣2D. ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D,E在圆上,四边形BCDE为矩形,这个矩形的面积是( )

A.2
B.
C.
D.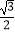
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x+m的图象与x轴的一个交点的坐标是(﹣1,0),则图象与x轴的另一个交点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=72°,∠C=30°,①求∠BAE的度数;②求∠DAE的度数;
(2)探究:如果只知道∠B=∠C+42°,也能求出∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三个顶点的坐标分别是A(3,3),B(1,1),C(4,–1).
(1)直接写出点A、B、C关于x轴对称的点A1、B1、C1的坐标;A1(__________)、B1(__________)、C1(__________).
(2)在图中作出△ABC关于y轴对称的图形△A2B2C2.
(3)求△ABC的面积.

相关试题

