【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点![]() 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( )
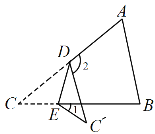
A. 80°B. 90°
C. 100°D. 110°
参考答案:
【答案】C
【解析】
先根据平角的定义和翻折变换的性质求出∠DEC,再根据三角形内角和定理求出∠CDE,即可得出答案.
解:∠A=65°,∠B=75°,∴∠C=∠C’ =180°-∠A-∠B=40°,
由翻折变换的性质可得:∠DEC=∠DEC’,
∠DEC+∠DEB=∠DEC+∠DEC’-∠1=180°,
∴∠DEC=100°,
∴∠CDE=∠EDC’=180°-∠C-∠DEC=40°,
∴∠2=180°-∠CDE-∠EDC’=100°.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠A=100°,BD平分∠ABC,求证:BC=BD+AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在
 中,
中,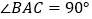 ,
,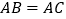 ,直线
,直线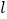 经过点
经过点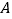 ,
,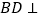 直线
直线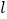 ,
,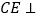 直线
直线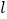 ,垂足分别为点
,垂足分别为点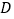 、
、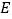 .证明:
.证明: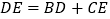 .
.(2)如图(2),将(1)中的条件改为:在
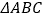 中,
中,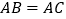 ,
,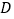 、
、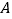 、
、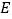 三点都在直线
三点都在直线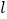 上,且
上,且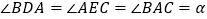 ,其中
,其中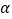 为任意锐角或钝角.请问结论
为任意锐角或钝角.请问结论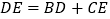 是否仍然成立?如成立;请你给出证明;若不成立,请说明理由.
是否仍然成立?如成立;请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),
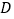 、
、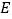 是直线
是直线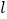 上的两动点
上的两动点 、
、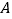 、
、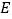 三点互不重合),点
三点互不重合),点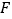 为
为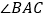 平分线上的一点,且
平分线上的一点,且 和
和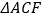 均为等边三角形,连接
均为等边三角形,连接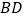 、
、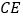 ,若
,若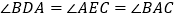 ,求证:
,求证: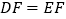 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距20千米,甲、乙两人都从A地去B地,图中射线l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.
下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米/小时,乙的速度是6千米/小时;
④乙先到达B地.其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数a使得关于x的不等式组
 ,有且仅有四个整数解,且使关于y的分式方程
,有且仅有四个整数解,且使关于y的分式方程 =1有整数解,则所有满足条件的整数a的值之和是( )
=1有整数解,则所有满足条件的整数a的值之和是( )A. 3B. 2C. ﹣2D. ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D,E在圆上,四边形BCDE为矩形,这个矩形的面积是( )

A.2
B.
C.
D.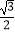
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为2,CD为AB边上的中线,E为线段CD上的动点,以BE为边,在BE左侧作等边△BEF,连接DF,则DF的最小值为_____.

相关试题

