【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,顶点B的坐标为(n,2),点E是AB的中点,在OA上取一点D,将△BAD沿BD翻折,点A刚好落在BC边上的F处,BD、EF交于点P
(1)直接写出点E、F的坐标;
(2)若OD=1,求P点的坐标;
(3)动点Q从P点出发,依次经过F,y轴上的点M,x轴上的点N,然后返回到P点:
①若要使Q点运动一周的路径最短,试确定M、N的位置;
②若n=3,求最短路径的四边形PFMN的周长.

参考答案:
【答案】(1)E(n,1);F(n-2,2);(2)点P坐标为(![]() ,
,![]() );(3)①见解析,②
);(3)①见解析,②![]() +
+![]() .
.
【解析】
(1)由翻折知四边形ABFD是正方形,据此得DF=AB=AD=2、OD=CF=BC-BF=n-2,即可得出点F坐标,由E为AB中点可得点E的坐标;
(2)OD=1知n=3,据此得出点B、D、E、F的坐标,分别求得直线BD和直线EF的解析式,联立方程组即可求得BD与EF的交点P的坐标;
(3)①作点F关于y轴的对称点F′、作点P关于x轴的对称点P′,连接F′P′交y轴于点M、交x轴于点N;
②由n=3结合(2)知点P、F及其关于坐标轴的对称点,利用勾股定理求解可得.
(1)∵B(n,2),
∴AB=OC=2、OA=BC=n,
由翻折知△DAB≌△DFB,
∴∠DAB=∠DFB=90°、BA=BF=2,
∵∠ABF=90°,
∴四边形ABFD是正方形,
∴DF=AB=AD=2,
∴OD=CF=BC-BF=n-2,
则F(n-2,2),
∵E为AB中点,
∴AE=BE=1,
∴E(n,1);
(2)若OD=1,则n-2=1,即n=3,
∴B(3,2)、D(1,0)、E(3,1)、F(1,2),
设BD所在直线解析式为y=kx+b,
将点B(3,2)、D(1,0)代入,得:
![]() ,
,
解得:![]() ,
,
∴BD所在直线解析式为y=x-1;
设EF所在直线解析式为y=mx+n,
将E(3,1)、F(1,2)代入,得:![]() ,
,
解得: ,
,
∴EF所在直线解析式为y=-![]() x+
x+![]() ;
;
由 可得
可得![]() ,
,
所以点P坐标为(![]() ,
,![]() );
);
(3)①如图所示,作点F关于y轴的对称点F′、作点P关于x轴的对称点P′,连接F′P′交y轴于点M、交x轴于点N,

②若n=3,由(2)知P(![]() ,
,![]() )、F(1,2),
)、F(1,2),
则F′(-1,2)、P′(![]() ,-
,-![]() ),
),
∴PF=![]() =
=![]() ,P′F′=
,P′F′=![]() =
=![]() ,
,
∴C四边形PFMN=![]() +
+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
(1)求证:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AD⊥BC于点D,∠1=∠2,∠CDG=∠B,
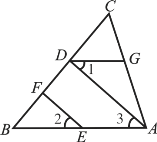
(1)能否得出DG∥BA?试说明理由.(2)EF与BC有什么关系?试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,点P在AD上,AB=
 ,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图).
,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图).
(1)当点E与点B重合时,点F恰好与点C重合(如图),则PC的长为 ;
(2)将直角尺从如图中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,从开始到停止,线段EF的中点所经过的路径(线段)长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近期猪肉价格不断走高,引起市民与政府的高度关注,当市场猪肉的平均价格达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%,某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日猪肉价格为每千克40元,5月21日,某市决定投入储备猪肉,并规定其销售价格在5月20日每千克40元的基础上下调a%出售,某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的
 ,两种猪肉销售的总金额比5月20日提高了
,两种猪肉销售的总金额比5月20日提高了 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按
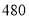 元销售时,每天可销售
元销售时,每天可销售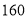 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出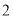 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为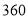 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润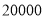 元?
元?
相关试题

