【题目】如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15o,E为AD延长线上的一点,且CE=CA,若点M在DE上,且DC=DM。则下列结论:①∠ADB=120°;②△ADC≌△BDC;③线段DC所在的直线垂直平分AB;④ME=BD;正确的有( )
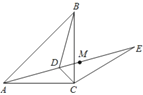
A. 1个B. 4个C. 2个D. 3个
参考答案:
【答案】B
【解析】
连接CM,求出∠DAB=∠DBA=30°,即可得∠ADB=120°;求出AD=BD,可证△ADC≌△BDC;求出∠ACD=∠BCD=45°,根据等腰三角形三线合一可得线段DC所在的直线垂直平分AB;求出∠MDC=60°,得等边三角形CMD,得出CM=CD,求出∠EMC=∠ADC=120°,证△ADC≌△EMC,推出AD=EM即可.
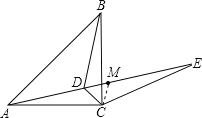
解:连接MC,在等腰直角△ABC中,
∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=45°-15°=30°,
∴∠ADB=120°,故①正确;
∴BD=AD,
又∵AC=BC,∠CAD=∠CBD=15°,
∴△BDC≌△ADC(SSS),故②正确;
∴∠DCA=∠DCB=45°,即CD平分∠BCA,
∴线段DC所在的直线垂直平分AB,(等腰三角形三线合一),故③正确;
∴∠EDC=∠DAC+∠DCA=15°+45°=60°,
∵DC=DM,
∴△MDC是等边三角形,即CM=CD.
又∵∠EMC=180°-∠DMC=180°-60°=120°,
∠ADC=180°-∠MDC=180°-60°=120°,
∴∠EMC=∠ADC.
又∵CE=CA,
∴∠DAC=∠CEM=15°,
∴△ADC≌△EMC(AAS),
∴ME=AD=DB,
∴ME=BD,故④正确.
正确的有:①②③④.
故选B.
-
科目: 来源: 题型:
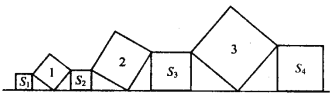
查看答案和解析>>【题目】如图,已知斜放着的3个正方形面积分别为1,2,3,正放着的4个正方形的面积依次为S1,S2,S3,S4,求S1+S2+S3+S4的值.
-
科目: 来源: 题型:
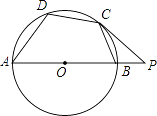
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某鞋店销售了9双鞋,各种尺码的销售量如下:
鞋的尺码
20
21
22
23
销售量(双)
1
2
4
2
(1)计算这9双鞋尺码的平均数、中位数和众数.
(2)哪一个指标是鞋厂最感兴趣的指标?哪一个指标是鞋厂最不感兴趣的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组积的科学家素养竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为90分、80分、70 分、60 分,学校将八年级(1)班和(2) 班的成绩整理并绘制成如下的统计图:
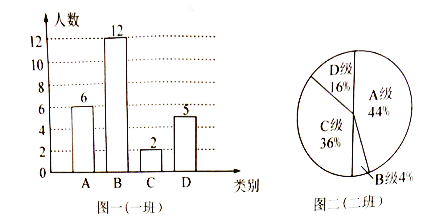
请你根据以上提供的信息解答下列问题:
(1) 此次竞赛中二 班成绩在70分以上(包括70分) 的人数有多少人?
(2) 补全下表中空缺的三个统计量:
平均数/ 分
中位数/ 分
众数/ 分
一班
77.6
80
_____________
二班
_____________
______________
90
(3) 请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中∠ABC=90°,AD平分∠BAC,点M、N分别是AD,AB上一动点,当AC=6时,BM+MN的最小值等于_______。

-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应区“美丽广西 清洁乡村”的号召,某校开展“美丽广西 清洁校园”的活动,该校经过精心设计,计算出需要绿化的面积为498m2 , 绿化150m2后,为了更快的完成该项绿化工作,将每天的工作量提高为原来的1.2倍.结果一共用20天完成了该项绿化工作.该项绿化工作原计划每天完成多少m2?
相关试题

